In linear algebra, the quotient of a vector space V {\displaystyle V} by a subspace N {\displaystyle N} is a vector space obtained by "collapsing" N {\displaystyle...

defining quotient objects (also called quotient algebras in universal algebra, and cokernels in category theory). For many types of algebraic structure...

specifically in linear algebra, a linear subspace or vector subspace is a vector space that is a subset of some larger vector space. A linear subspace is...

as spaces. In particular: Quotient space (topology), in case of topological spaces Quotient space (linear algebra), in case of vector spaces Quotient space...

group Quotient space (linear algebra) – Vector space consisting of affine subsets Mapping cone (homological algebra) – Tool in homological algebra Brown...

quotient rings of ring theory, quotient groups of group theory, the quotient spaces of linear algebra and the quotient modules of representation theory...

conjugate transpose, and linear operators over a Hilbert space and Hermitian adjoints. However, it may happen that an algebra admits no involution. Look...

linear group of a vector space V on the associated projective space P(V). Explicitly, the projective linear group is the quotient group PGL(V) = GL(V) / Z(V)...

and to the quotient space in linear algebra. It is a specific example of a quotient, as viewed from the general setting of universal algebra. Starting...

structure, the quotient set often inherits a similar structure from its parent set. Examples include quotient spaces in linear algebra, quotient spaces in topology...

concept of vector spaces is fundamental for linear algebra, together with the concept of matrices, which allows computing in vector spaces. This provides...

A particular case is that of a complex algebra A of continuous linear operators on a complex Hilbert space with two additional properties: A is a topologically...

{\displaystyle M} is a closed linear subspace of a normed space X , {\displaystyle X,} there is a natural norm on the quotient space X / M , {\displaystyle X/M...

the algebraic dual space. When defined for a topological vector space, there is a subspace of the dual space, corresponding to continuous linear functionals...

set by an equivalence relation Quotient group Quotient ring Quotient module Quotient space (linear algebra) Quotient space (topology), by an equivalence...

topological space. A straightforward argument involving elementary linear algebra shows that the only finite-dimensional seminormed spaces are those arising...

mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure...

In algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is very similar to that of a...

In mathematics, the exterior algebra or Grassmann algebra of a vector space V {\displaystyle V} is an associative algebra that contains V , {\displaystyle...

In mathematics, the kernel of a linear map, also known as the null space or nullspace, is the part of the domain which is mapped to the zero vector of...

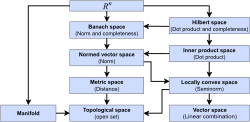
basic spaces are linear spaces (also called vector spaces) and topological spaces. Linear spaces are of algebraic nature; there are real linear spaces (over...

In mathematics, a Lie algebra (pronounced /liː/ LEE) is a vector space g {\displaystyle {\mathfrak {g}}} together with an operation called the Lie bracket...

symmetric algebra over V can be viewed as a "coordinate free" polynomial ring over V. The symmetric algebra S(V) can be built as the quotient of the tensor...

vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over K. A standard first example of a K-algebra is...

authors, especially in physics and matrix algebra, prefer to define inner products and sesquilinear forms with linearity in the second argument rather than the...

which is more often encountered in modern textbooks. Using linear algebra, a projective space of dimension n is defined as the set of the vector lines (that...

vector space (called vectors). Abstract algebra is the name that is commonly given to the study of algebraic structures. The general theory of algebraic structures...

branch of mathematics, an operator algebra is an algebra of continuous linear operators on a topological vector space, with the multiplication given by...

the following application to linear algebra. Let V be a finite-dimensional vector space over a field k and f : V → V a linear map with minimal polynomial...

be an affine space, and D be a linear subspace of the associated vector space E → {\displaystyle {\overrightarrow {E}}} . The quotient E/D of E by D...