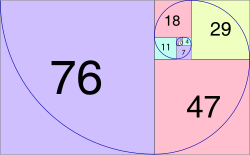
There are a number of possible generalizations of the Fibonacci numbers which include the real numbers (and sometimes the complex numbers) in their domain...

the Fibonacci sequence is a sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence...

mathematics, the Fibonacci polynomials are a polynomial sequence which can be considered as a generalization of the Fibonacci numbers. The polynomials...

closely related Fibonacci sequence. Individual numbers in the Lucas sequence are known as Lucas numbers. Lucas numbers and Fibonacci numbers form complementary...

sequence of Fibonacci numbers taken modulo n repeats. Pisano periods are named after Leonardo Pisano, better known as Fibonacci. The existence of periodic...

integers based on Fibonacci numbers. Each code word ends with "11" and contains no other instances of "11" before the end. The Fibonacci code is closely...

The reciprocal Fibonacci constant ψ is the sum of the reciprocals of the Fibonacci numbers: ψ = ∑ k = 1 ∞ 1 F k = 1 1 + 1 1 + 1 2 + 1 3 + 1 5 + 1 8 +...

This is a list of articles about prime numbers. A prime number (or prime) is a natural number greater than 1 that has no positive divisors other than...

concatenation in the same way that the Fibonacci numbers are formed by repeated addition. It is a paradigmatic example of a Sturmian word and specifically,...

such as the sequence of Fibonacci numbers, the sequence of factorials, the sequence of perfect numbers, and so forth, many of which are enumerated in...

(2025): The generalized k-Leonardo numbers: a non-homogeneous generalization of the Fibonacci numbers, Palestine Journal of Mathematics, 14. 1. P. Catarino...

natural numbers such that a × b = 0, then a = 0 or b = 0 (or both). Two important generalizations of natural numbers arise from the two uses of counting...

Fibonacci number Fibonacci word List of fractals by Hausdorff dimension Ramírez, José L.; Rubiano, Gustavo N. (2014). "Properties and Generalizations...

In mathematics, the random Fibonacci sequence is a stochastic analogue of the Fibonacci sequence defined by the recurrence relation f n = f n − 1 ± f n...

) correspond to the original factoriangular numbers. Doubly triangular number Factorial prime Fibonacci number Lazy caterer's sequence Square triangular...

them. Example of such sets of integers are Fibonacci numbers and perfect numbers. For more examples, see Integer sequence. Algebraic numbers are those that...

any expression. Prime numbers Sequences Fibonacci numbers Generalizations of Fibonacci numbers Geometric progressions Arithmetic progression Recurrence...

integer multiple of ⁠ p {\displaystyle p} ⁠. Carmichael numbers are composite numbers which have the same property. Carmichael numbers are also called...

sequential Fibonacci numbers, suggesting a generalization of the dissection scheme based on Fibonacci numbers. The properties of the Fibonacci numbers also...

time, where | V | {\displaystyle |V|} is the number of nodes. Fredman & Tarjan 1984 proposed a Fibonacci heap priority queue to optimize the running time...

that the sieve of Eratosthenes can be sped up by considering only the prime divisors up to the square root of the upper limit. Fibonacci took the innovations...

The prime numbers are widely used in mathematics, particularly in number theory where many results related to them exist. The Fibonacci numbers comprise...

generalized shift register and Lagged Fibonacci generators. Mersenne primes Mp are closely connected to perfect numbers. In the 4th century BC, Euclid proved...

The Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named...

as the properties of mathematical objects constructed from integers (for example, rational numbers), or defined as generalizations of the integers (for...

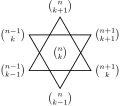
28, 8) = 2. This result in turn has further generalizations. The two sets of three numbers which the Star of David theorem says have equal greatest common...

problem" of geometric probability. The Sylvester expansion or Fibonacci–Sylvester expansion of a rational number, a representation as a sum of unit fractions...

McDaniel, Wayne L. (1982). "Representations of every integer as the difference of powerful numbers". Fibonacci Quarterly. 20: 85–87. doi:10.1080/00150517...

Iekata (1997). "Transcendence of Rogers-Ramanujan continued fraction and reciprocal sums of Fibonacci numbers". Proceedings of the Japan Academy, Series A...

condensed matter physics, a Fibonacci anyon is a type of anyon which lives in two-dimensional topologically ordered systems. The Fibonacci anyon τ {\displaystyle...