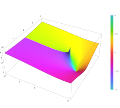
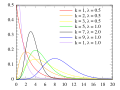
In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems...

mathematics, the gamma function (represented by Γ, capital Greek letter gamma) is the most common extension of the factorial function to complex numbers...

the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial...

mathematics, the upper incomplete gamma function The Christoffel symbols in differential geometry In probability theory and statistics, the gamma distribution is...

mathematicians defined this type incomplete-version of Bessel function or this type generalized-version of incomplete gamma function: K v ( x , y ) = ∫ 1 ∞ e...

{\gamma (\alpha ,\lambda x)}{\Gamma (\alpha )}},} where γ ( α , λ x ) {\displaystyle \gamma (\alpha ,\lambda x)} is the lower incomplete gamma function...

{z^{k}}{k^{s}}}~{\frac {\Gamma (s,kb)}{\Gamma (s)}}} where Γ(s) is the gamma function and Γ(s,x) is the upper incomplete gamma function. Since Γ(s,0)=Γ(s),...

t ( e t − 1 ) 2 = ∑ k = 0 ∞ k e k t . {\displaystyle {\frac {e^{t}}{(e^{t}-1)^{2}}}=\sum _{k=0}^{\infty }k\,e^{kt}.} Incomplete gamma function v t e...

}{x}}\right)}{\Gamma (\alpha )}}=Q\left(\alpha ,{\frac {\beta }{x}}\right)\!} where the numerator is the upper incomplete gamma function and the denominator...

{\displaystyle \Gamma (s,y)} is the upper incomplete gamma function. Since Γ ( s , 0 ) = Γ ( s ) {\displaystyle \Gamma (s,0)=\Gamma (s)} , it follows that: F j ⁡...

function, Polygamma function Incomplete beta function Incomplete gamma function K-function Multivariate gamma function: A generalization of the Gamma...

t-t\ln z)}{(1+t^{2})^{s/2}(e^{2\pi t}-1)}}dt} where Γ is the upper incomplete gamma-function. All (but not part) of the ln(z) in this expression can be replaced...

the lower incomplete gamma function, and P ( ⋅ , ⋅ ) {\displaystyle P(\cdot ,\cdot )} denotes the regularized lower incomplete gamma function. The quantile...

[further explanation needed] In terms of the regularized gamma function P and the incomplete gamma function, erf ⁡ x = sgn ⁡ x ⋅ P ( 1 2 , x 2 ) = sgn ⁡ x π γ...

theory and the tabulation of the Incomplete gamma function, where he wrote the book “Tables of the Incomplete Gamma Function Ratio”.[citation needed] He contributed...

using the incomplete gamma function. If Q ( a , z ) = Γ ( a , z ) Γ ( a ) = 1 Γ ( a ) ∫ z ∞ u a − 1 e − u d u {\displaystyle Q(a,z)={\frac {\Gamma (a,z)}{\Gamma...

π ) {\displaystyle -(\Gamma (0,-\ln 2)+i\,\pi )} where Γ ( a , x ) {\displaystyle \Gamma (a,x)} is the incomplete gamma function. It must be understood...

polynomials Incomplete gamma function Laguerre polynomials Parabolic cylinder function (or Weber function) Poisson–Charlier function Toronto functions Whittaker...

Schechter function with α = − 1 {\displaystyle \alpha =-1} is said to be flat. Integrals of the Schechter function can be expressed via the incomplete gamma function...

identities Hypergeometric series Incomplete beta function Incomplete gamma function Jordan–Pólya number Kempner function Lah number Lanczos approximation...

}{1-\alpha }}\Gamma \left(1+{\frac {1}{k}},-\ln(1-\alpha )\right)} , where Γ ( s , x ) {\displaystyle \Gamma (s,x)} is the upper incomplete gamma function. If the...

j-1}&{\text{otherwise}}\end{cases}}} and Γ(x,y) is the upper incomplete gamma function. ∫ 1 a e λ x + b d x = x b − 1 b λ ln ⁡ ( a e λ x + b ) {\displaystyle...

yields many interesting series in mathematics, for example the incomplete gamma function has the asymptotic expansion Γ ( a , z ) ∼ z a − 1 e − z ( 1 +...

special case of the upper incomplete gamma function: E n ( x ) = x n − 1 Γ ( 1 − n , x ) . {\displaystyle E_{n}(x)=x^{n-1}\Gamma (1-n,x).} The generalized...

|a|<1;\Re (s)<0;z\notin (0,\infty ).} An asymptotic series in the incomplete gamma function Φ ( z , s , a ) = 1 2 a s + 1 z a ∑ k = 1 ∞ e − 2 π i ( k − 1...

(-ix_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-ix_{\mathrm {m} }t),} where Γ(a, x) is the incomplete gamma function. The parameters may be solved for...

{x^{m+nl+1}}{l!}}} is a confluent hypergeometric function and also an incomplete gamma function ∫ x m e i x n d x = x m + 1 m + 1 1 F 1 ( m + 1 n 1...

}}\Re (\gamma )>-{\tfrac {1}{2}}} for the exponential function. The incomplete gamma function has the representation Γ ( α , x ) = x α e − x ∑ i = 0...

optical mode in a waveguide the gamma function, a generalization of the factorial the upper incomplete gamma function the modular group, the group of...

antiderivatives, the special functions (like the Legendre functions, the hypergeometric function, the gamma function, the incomplete gamma function and so on). Extending...