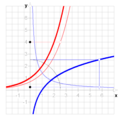
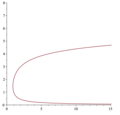
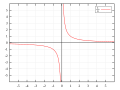
mathematics, the inverse function of a function f (also called the inverse of f) is a function that undoes the operation of f. The inverse of f exists if...

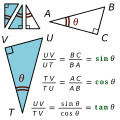
mathematics, the inverse trigonometric functions (occasionally also called antitrigonometric, cyclometric, or arcus functions) are the inverse functions of the...

inverse function. The inverse function is also differentiable, and the inverse function rule expresses its derivative as the multiplicative inverse of...

mathematics, the inverse hyperbolic functions are inverses of the hyperbolic functions, analogous to the inverse circular functions. There are six in...

calculus, the inverse function rule is a formula that expresses the derivative of the inverse of a bijective and differentiable function f in terms of...

interval I, it has an inverse function, which is a real function with domain f(I) and image I. This is how inverse trigonometric functions are defined in terms...

In mathematics, the inverse gamma function Γ − 1 ( x ) {\displaystyle \Gamma ^{-1}(x)} is the inverse function of the gamma function. In other words, y...

percentile function (after the percentile), percent-point function, inverse cumulative distribution function (after the cumulative distribution function or c...

from any probability distribution given its cumulative distribution function. Inverse transformation sampling takes uniform samples of a number u {\displaystyle...

mathematics, integrals of inverse functions can be computed by means of a formula that expresses the antiderivatives of the inverse f − 1 {\displaystyle f^{-1}}...

The reciprocal function, the function f(x) that maps x to 1/x, is one of the simplest examples of a function which is its own inverse (an involution)...

mathematics, an involution, involutory function, or self-inverse function is a function f that is its own inverse, f(f(x)) = x for all x in the domain of...

trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related...

considered above grows very rapidly, its inverse function, f−1, grows very slowly. This inverse Ackermann function f−1 is usually denoted by α. In fact,...

the implicit function theorem. Inverse function theorem Constant rank theorem: Both the implicit function theorem and the inverse function theorem can...

notion is rarely used. Image and inverse image may also be defined for general binary relations, not just functions. The word "image" is used in three...

\end{aligned}}} The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as probit...

sine and cosine are not injective, their inverses are not exact inverse functions, but partial inverse functions. For example, sin ⁡ ( 0 ) = 0 {\displaystyle...

In economics, an inverse demand function is the mathematical relationship that expresses price as a function of quantity demanded (it is therefore also...

real-valued function of a positive real variable, is the inverse function of the exponential function, leading to the identities: e ln ⁡ x = x  if  x ∈ R +...

F(x)=p} . This defines the inverse distribution function or quantile function. Some distributions do not have a unique inverse (for example if f X ( x )...

integers to the even numbers, which has the division by two as its inverse function. A function is bijective if and only if it is both injective (or one-to-one)—meaning...

written logb x, so log10 1000 = 3. As a single-variable function, the logarithm to base b is the inverse of exponentiation with base b. The logarithm base 10...

implicit function is an inverse function. Not all functions have a unique inverse function. If g is a function of x that has a unique inverse, then the...

/2}}}}} . The quantile function of a distribution is the inverse of the cumulative distribution function. The quantile function of the standard normal...

trigonometric functions. The inverse hyperbolic functions are: inverse hyperbolic sine "arsinh" (also denoted "sinh−1", "asinh" or sometimes "arcsinh") inverse hyperbolic...

domain. Every surjective function has a right inverse assuming the axiom of choice, and every function with a right inverse is necessarily a surjection...

exponential function is the inverse function of the natural logarithm. The inverse function theorem implies that the natural logarithm has an inverse function, that...

follows that the composition of two bijections is also a bijection. The inverse function of a composition (assumed invertible) has the property that (f ∘ g)−1...

5^{2}(2-k^{2})+z^{2}-{}}}\cdots } The inverses of the Jacobi elliptic functions can be defined similarly to the inverse trigonometric functions; if x = sn ⁡ ( ξ , m )...