Axiomatic constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. The same first-order language...

Constructivism also includes the study of constructive set theories such as CZF and the study of topos theory. Constructivism is often identified with...

Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any...

set theory Constructive set theory Zermelo set theory General set theory Mac Lane set theory Non-well-founded set theory List of first-order theories...

In mathematical physics, constructive quantum field theory is the field devoted to showing that quantum field theory can be defined in terms of precise...

of constructive theories such as Heyting arithmetic and constructive set theories (Rathjen 2005). The disjunction property is satisfied by a theory if...

Intuitionistic type theory (also known as constructive type theory, or Martin-Löf type theory (MLTT)) is a type theory and an alternative foundation of...

set theories: Morse–Kelley set theory Von Neumann–Bernays–Gödel set theory Tarski–Grothendieck set theory Constructive set theory Internal set theory...

is not valid in constructive or intuitionistic logic, and so this separate terminology is mostly used in the set theory of constructive mathematics. In...

axiom of set theory. Informally put, the axiom of choice says that given any collection of non-empty sets, it is possible to construct a new set by choosing...

assumed. The proof below is therefore given using the means of a constructive set theory. It is evident from the proof how the theorem relies on the axiom...

Constructive set theory (e.g., CZF — Constructive Zermelo–Fraenkel set theory): Builds sets constructively. Realizability Theory: Ties constructive logic...

proofs were essentially constructive. The first non-constructive constructions appeared with Georg Cantor’s theory of infinite sets, and the formal definition...

axiom of power set appears in most axiomatizations of set theory. It is generally considered uncontroversial, although constructive set theory prefers a weaker...

between KP, generalized recursion theory, and the theory of admissible ordinals. KP can be studied as a constructive set theory by dropping the law of excluded...

Cantor's first set theory article contains Georg Cantor's first theorems of transfinite set theory, which studies infinite sets and their properties. One...

KP; Pocket set theory General set theory, GST Constructive set theory, CZF Mac Lane set theory and Elementary topos theory Zermelo set theory; Z Zermelo–Fraenkel...

Manchester. He is known for his work in non-well-founded set theory, constructive set theory, and Frege structures. Aczel completed his Bachelor of Arts...

hierarchy. Bounded quantifiers are important in Kripke–Platek set theory and constructive set theory, where only Δ0 separation is included. That is, it includes...

mathematics and set theory, hereditarily finite sets are defined as finite sets whose elements are all hereditarily finite sets. In other words, the set itself...

In set theory, the complement of a set A, often denoted by A c {\displaystyle A^{c}} (or A′), is the set of elements not in A. When all elements in the...

techniques from recursion theory as well as proof theory. Functional interpretations are interpretations of non-constructive theories in functional ones. Functional...

Consequentia mirabilis – Pattern of reasoning in propositional logic Constructive set theory Diaconescu's theorem Dichotomy – Splitting of a whole into exactly...

"Set Theory", Stanford Encyclopedia of Philosophy, Metaphysics Research Lab, Stanford University Suppes, Patrick (1972) [1960], Axiomatic Set Theory,...

In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations...

type theories serve as alternatives to set theory as a foundation of mathematics. Two influential type theories that have been proposed as foundations...

intuitionistic analogue of Boolean algebras. BHK interpretation Constructive analysis Constructive set theory Harrop formula Realizability Troelstra 1973:18 Sørenson...

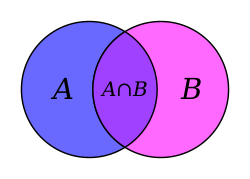
In set theory, the intersection of two sets A {\displaystyle A} and B , {\displaystyle B,} denoted by A ∩ B , {\displaystyle A\cap B,} is the set containing...

discrete and Euclidean geometries, graph theory, group theory, model theory, number theory, set theory, Ramsey theory, dynamical systems, and partial differential...

in set theory, the constructible universe (or Gödel's constructible universe), denoted by L , {\displaystyle L,} is a particular class of sets that...