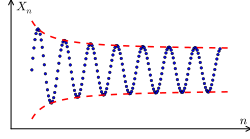
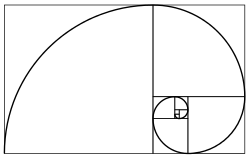
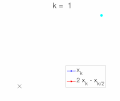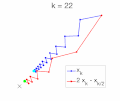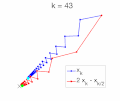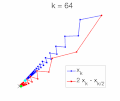
In mathematics, a recurrence relation is an equation according to which the n {\displaystyle n} th term of a sequence of numbers is equal to some combination...

dynamical systems), a linear recurrence with constant coefficients: ch. 17 : ch. 10  (also known as a linear recurrence relation or linear difference equation)...

linear three-term recurrence relation (TTRR, the qualifiers "homogeneous linear" are usually taken for granted) is a recurrence relation of the form y n...

entries would all be 0. Stirling numbers of the second kind obey the recurrence relation (first discovered by Masanobu Saka in his 1782 Sanpō-Gakkai): { n...

memory. The Thue–Morse sequence is the sequence tn satisfying the recurrence relation t 0 = 0 , t 2 n = t n , t 2 n + 1 = 1 − t n , {\displaystyle...

sequence of probabilist's Hermite polynomials also satisfies the recurrence relation He n + 1 ⁡ ( x ) = x He n ⁡ ( x ) − He n ′ ⁡ ( x ) . {\displaystyle...

is the case for Gaussian quadrature), the recurrence relation reduces to a three-term recurrence relation: For s < r − 1 , x p s {\displaystyle s<r-1...

applications of the recurrence relation. The Fibonacci sequence is a simple classical example, defined by the recurrence relation a n = a n − 1 + a n...

number V n {\displaystyle V_{n}} can be expressed via a two-dimension recurrence relation. Closed-form expressions involve the gamma, factorial, or double...

G6 through a recurrence relation. Let dk = (2k + 3)k! G2k + 4, so for example, d0 = 3G4 and d1 = 5G6. Then the dk satisfy the relation ∑ k = 0 n ( n...

k}\right].} The unsigned Stirling numbers of the first kind follow the recurrence relation [ n + 1 k ] = n [ n k ] + [ n k − 1 ] {\displaystyle \left[{n+1 \atop...

applies to any class of functions that can be defined by a three-term recurrence relation. In full generality, the Clenshaw algorithm computes the weighted...

_{n=0}^{\infty }a_{n}x^{n}.} A recurrence relation defines each term of a sequence in terms of the preceding terms. Recurrence relations may lead to previously...

numbers are also closely related to Lucas numbers, which obey the same recurrence relation and with the Fibonacci numbers form a complementary pair of Lucas...

\choose k}\!\!\right)=\left(\!\!{k+1 \choose n-1}\!\!\right).} A recurrence relation for multiset coefficients may be given as ( ( n k ) ) = ( ( n k −...

\lfloor K/2\rfloor } , N). In aid of this, we have the following recurrence relation: p(i, j) is True if either p(i, j − 1) is True or if p(i − xj, j...

Recurrence plot, a statistical plot that shows a pattern that re-occurs Recurrence relation, an equation which defines a sequence recursively Recurrent rotation...

the master theorem for divide-and-conquer recurrences provides an asymptotic analysis for many recurrence relations that occur in the analysis of divide-and-conquer...

case above but which has an extra term ⁠e−t/t⁠. It satisfies the recurrence relation ψ ( m ) ( z + 1 ) = ψ ( m ) ( z ) + ( − 1 ) m m ! z m + 1 {\displaystyle...

equation follows from the recurrence relation by expanding both sides into power series. On the one hand, the recurrence relation uniquely determines the...

linear recurrence relation of the form x k = n x k − 1 + x k − 2 . {\displaystyle x_{k}=nx_{k-1}+x_{k-2}.} It follows that, given such a recurrence the solution...

as a recurrence relation: b n = n b n − 1 {\displaystyle b_{n}=nb_{n-1}} b 0 = 1 {\displaystyle b_{0}=1} This evaluation of the recurrence relation demonstrates...

Zeckendorf's theorem, or directly from the golden ratio and the recurrence relation defining the Fibonacci numbers. The Wythoff array has the values...

given expression with the determinant. The polynomials Pn satisfy a recurrence relation of the form P n ( x ) = ( A n x + B n ) P n − 1 ( x ) + C n P n −...

{\displaystyle {\frac {d}{dx}}[(1-x^{2})\,y']+\lambda \,y=0.} The recurrence relation is ( n + 1 ) P n + 1 ( x ) = ( 2 n + 1 ) x P n ( x ) − n P n − 1...

extend to their holomorphic counterparts. Repeated application of the recurrence relation for the lower incomplete gamma function leads to the power series...

{t^{k_{0}}A_{0}\left({\frac {h}{t}}\right)-A_{0}(h)}{t^{k_{0}}-1}}.} A general recurrence relation can be defined for the approximations by A i + 1 ( h ) = t k i A...

consistent amount of times. An alternative approach is to set up a recurrence relation for the T(n) factor, the time needed to sort a list of size n. In...

Bunyakovsky conjecture. Another prime generator is defined by the recurrence relation a n = a n − 1 + gcd ( n , a n − 1 ) , a 1 = 7 , {\displaystyle a_{n}=a_{n-1}+\gcd(n...

word size (in number of bits) n: degree of recurrence m: middle word, an offset used in the recurrence relation defining the series x {\displaystyle x} ...