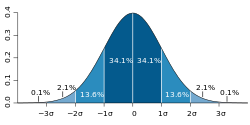
In computing, a roundoff error, also called rounding error, is the difference between the result produced by a given algorithm using exact arithmetic...

floating-point difference is computed exactly, by the Sterbenz lemma—there is no rounding error introduced by the floating-point subtraction operation. Formally, catastrophic...

not the numbers that it displays. Moreover, the error in Excel's answer is not simply round-off error, it is an effect in floating point calculations...

123500". On the other hand, rounding of exact numbers will introduce some round-off error in the reported result. Rounding is almost unavoidable when reporting...

An off-by-one error or off-by-one bug (known by acronyms OBOE, OBO, OB1 and OBOB) is a logic error that involves a number that differs from its intended...

accuracy, leading to unavoidable truncation or rounding. Another common source is inherent measurement error, stemming from the practical limitations of...

an input value and its quantized value (such as round-off error) is referred to as quantization error, noise or distortion. A device or algorithmic function...

resolution in the range (values), nor in round-off error arising from floating-point arithmetic. Discretization error would occur even if it were possible...

stability if the conjugate gradient method misbehaves, e.g., due to round-off error. The formulas x k + 1 := x k + α k p k {\displaystyle \mathbf {x} _{k+1}:=\mathbf...

Round-off error and is caused by the finite precision of computations involving floating-point numbers. The second, usually called Truncation error,...

algorithms for differential equations the concern is the growth of round-off errors and/or small fluctuations in initial data which might cause a large...

regained. The Kahan summation algorithm may be used to reduce the errors. Round-off error can affect the convergence and accuracy of iterative numerical...

2Sum is a floating-point algorithm for computing the exact round-off error in a floating-point addition operation. 2Sum and its variant Fast2Sum were...

floating-point numbers that substantially reduces the accumulated round-off error compared to naively accumulating the sum in sequence. Although there...

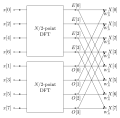
are computed with infinite precision. However, in the presence of round-off error, many FFT algorithms are much more accurate than evaluating the DFT...

show than convergence (and would be needed in any event to show that round-off error will not destroy the computation). Hence convergence is usually shown...

(BFGS). Loss of the positive-definite condition through round-off error is avoided if rather than updating an approximation to the inverse...

allow the algorithm to proceed successfully, and possibly to reduce round-off error. It is often used for verifying row echelon form. Pivoting might be...

two very nearly equal numbers (the case of large b), which causes round-off error in a numerical evaluation. The figure shows the difference between[clarification...

consider round-off error, arithmetic overflow, and arithmetic underflow. The method below calculates the running sums method with reduced rounding errors. This...

computation to reduce round-off error Truncation — rounding a floating-point number by discarding all digits after a certain digit Round-off error Numeric precision...

by mistake, round-off error (the consequence of using finite precision floating point numbers on computers), is also called truncation error, especially...

caused by limited sub-pixel precision, floating point and fixed point round-off errors. The more z-buffer precision one uses, the less likely it is that z-fighting...

the inverse of the error variance-covariance matrix of the observations. In the absence of round-off error and of experimental error in the independent...

algorithm Precision (computer science) Round-off error Lower, Stephen (2021-03-31). "Significant Figures and Rounding". Chemistry - LibreTexts. Chemistry...

(i.e. if its condition number multiplied by the machine's relative round-off error is appreciably large). In that case, including the smallest singular...

requires an ulp function Least significant bit (LSB) Machine epsilon Round-off error Goldberg, David (March 1991). "What Every Computer Scientist Should...

x , t ) {\displaystyle u(x,t)} of the PDE on the grid. Define the round-off error ϵ j n {\displaystyle \epsilon _{j}^{n}} as ϵ j n = N j n − u j n {\displaystyle...

and additions. Generally, it is important to estimate and control round-off errors arising from the use of floating-point arithmetic. Interpolation solves...

introduces division, which results in round-off errors when implemented using floating point numbers. Round-off errors can be avoided if all the numbers are...