of its namesake the Möbius inversion formula. Following work of Gian-Carlo Rota in the 1960s, generalizations of the Möbius function were introduced into...

Ferdinand Möbius. A large generalization of this formula applies to summation over an arbitrary locally finite partially ordered set, with Möbius' classical...

the zeta function is the Möbius function μ(a, b); every value of μ(a, b) is an integral multiple of 1 in the base ring. The Möbius function can also be...

Leipzig. Möbius died in Leipzig in 1868 at the age of 77. His son Theodor was a noted philologist. He is best known for his discovery of the Möbius strip...

Look up Möbius in Wiktionary, the free dictionary. Moebius, Mœbius, Möbius or Mobius may refer to: August Ferdinand Möbius (1790–1868), German mathematician...

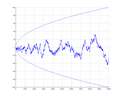
_{k=1}^{n}\mu (k),} where μ ( k ) {\displaystyle \mu (k)} is the Möbius function. The function is named in honour of Franz Mertens. This definition can be...

In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form f ( z ) = a z + b c z + d {\displaystyle...

=\varepsilon } , the Dirichlet inverse of the constant function 1 {\displaystyle 1} is the Möbius function (see proof). Hence: g = f ∗ 1 {\displaystyle g=f*1}...

has no prime factors, Ω(1) = 0, so λ(1) = 1. It is related to the Möbius function μ(n). Write n as n = a2b, where b is squarefree, i.e., ω(b) = Ω(b)...

{n}{d}}=n\sum _{d\mid n}{\frac {\mu (d)}{d}},} where μ is the Möbius function, the multiplicative function defined by μ ( p ) = − 1 {\displaystyle \mu (p)=-1} and...

its Möbius function, a goal first explicitly presented by Wilf (2002). The goal in such investigations is to find a formula for the Möbius function of...

indicator function may be defined. This is commonly called the generalized Möbius function, as a generalization of the inverse of the indicator function in elementary...

\left(x^{1/n}\right),} μ(n) is the Möbius function, li(x) is the logarithmic integral function, ρ indexes every zero of the Riemann zeta function, and li(x⁠ρ/n⁠) is not...

the Riemann zeta function. The generating function of the Möbius function is the inverse of the zeta function: ζ ( s ) ∑ n = 1 ∞ μ ( n ) n s = 1 , ℜ s...

zeta series. The reciprocal of the zeta function may be expressed as a Dirichlet series over the Möbius function μ(n): 1 ζ ( s ) = ∑ n = 1 ∞ μ ( n ) n s...

bigger than) n {\displaystyle n} μ ( n ) {\displaystyle \mu (n)} : the Möbius function, the parity ( − 1 {\displaystyle -1} for odd, + 1 {\displaystyle +1}...

of many other arithmetic functions, in addition to the primes counting function above. One example involves the Möbius function μ. The statement that the...

involving only the Möbius function, and the way it self-correlates. Peter Sarnak made a conjecture on the non-correlation of the Möbius function with more general...

constants. The function ω ( n ) {\displaystyle \omega (n)} is related to divisor sums over the Möbius function and the divisor function, including: ∑ d...

differential equations the degree of membership in a fuzzy set the Möbius function in number theory the population mean or expected value in probability...

\mu } denotes the Möbius function and k {\displaystyle k} denotes a positive integer, generalize the von Mangoldt function. The function Λ 1 {\displaystyle...

|\,n}\mu \left({n \over d}\right)\alpha ^{d},} and μ is the classic Möbius function of number theory. The name comes from the denominator, 1 − z j, which...

z)=\sum \limits _{d\mid P(z)}\mu (d)A_{d}(x)} by using the Möbius function and some functions A d ( x ) {\displaystyle A_{d}(x)} induced by the elements...

\mu \cdot f} where μ {\displaystyle \mu } is the Möbius function. Completely multiplicative functions also satisfy a distributive law. If f is completely...

arithmetic functions. The Möbius function μ {\displaystyle \mu } has μ p ( x ) = 1 − x . {\displaystyle \mu _{p}(x)=1-x.} The Mobius function squared has...

Mertens function is defined as M ( n ) = ∑ 1 ≤ k ≤ n μ ( k ) , {\displaystyle M(n)=\sum _{1\leq k\leq n}\mu (k),} where μ(k) is the Möbius function; the...

{\displaystyle \mu (n)} , which generally denotes the Möbius function). Möbius inversion formula Heaviside step function Kronecker delta Estrada, Ricardo (1995), "Dirichlet...

{\displaystyle \operatorname {SP} (n)=\mu (n),} where μ(n) is the Möbius function. In the section Elementary properties, it was shown that if R(n) is...

− 1 ) 2 x = 1 {\displaystyle \mu (n)=(-1)^{2x}=1} (where μ is the Möbius function and x is half the total of prime factors), while for the former μ (...

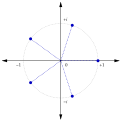
Möbius μ function: Sum of the nth primitive roots of unity, it depends on the prime factorization of n. Prime omega functions Chebyshev functions Liouville...