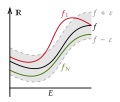
The Arzelà–Ascoli theorem is a fundamental result of mathematical analysis giving necessary and sufficient conditions to decide whether every sequence...

earlier by Giulio Ascoli in the Arzelà–Ascoli theorem. He was a pupil of the Scuola Normale Superiore of Pisa where he graduated in 1869. Arzelà came from a...

Ascoli and Cesare Arzelà. The culmination of their investigations, the Arzelà–Ascoli theorem, was a generalization of the Bolzano–Weierstrass theorem...

functions. In 1889, Italian mathematician Cesare Arzelà generalized Ascoli's Theorem into the Arzelà–Ascoli theorem, a practical sequential compactness criterion...

{\displaystyle f_{\psi (k)}} are equicontinuous by the Arzelà–Ascoli theorem. By the fundamental theorem of calculus, z ′ ( t ) = f ( t , z ( t ) ) {\displaystyle...

can be thought of as an Lp version of the Arzelà–Ascoli theorem, from which it can be deduced. The theorem is named after Maurice René Fréchet and Andrey...

total variation norm. Since Prokhorov's theorem expresses tightness in terms of compactness, the Arzelà–Ascoli theorem is often used to substitute for compactness:...

diagonalization argument similar to the one employed in the proof of the Arzelà–Ascoli theorem. Due to the constructive nature of its proof (as opposed to the...

(Riemannian geometry) Arzelà–Ascoli theorem (functional analysis) Baire category theorem (topology, metric spaces) Bing metrization theorem (general topology)...

Banach–Alaoglu theorem on the weak-* compactness of the unit ball of the dual space of a normed vector space, and the Arzelà–Ascoli theorem characterizing...

Dini's theorem Arzelà–Ascoli theorem Sørensen, Henrik Kragh (2005). "Exceptions and counterexamples: Understanding Abel's comment on Cauchy's Theorem". Historia...

role of this theorem in the theory of Gromov–Hausdorff convergence may be considered as analogous to the role of the Arzelà–Ascoli theorem in the theory...

with bounded Lipschitz constant forms an equicontinuous set. The Arzelà–Ascoli theorem implies that if {fn} is a uniformly bounded sequence of functions...

then the transpose T′ is compact. This can be proved using the Arzelà–Ascoli theorem. When V is a Hilbert space, there is an antilinear isomorphism iV...

compact set are precompact in the uniform topology; this is the Arzelà–Ascoli theorem. A metric space is separable if and only if it is homeomorphic to...

category theorem Open mapping theorem (functional analysis) Closed graph theorem Uniform boundedness principle Arzelà–Ascoli theorem Banach–Alaoglu theorem Measure...

norm, thus making C(X) a Banach space, hence a metric space. Then Arzelà–Ascoli theorem states that a subset of C(X) is compact if and only if it is closed...

Some major theorems characterize relatively compact subsets, in particular in function spaces. An example is the Arzelà–Ascoli theorem. Other cases...

Heine–Borel theorems, the intermediate value theorem and mean value theorem, Taylor's theorem, the fundamental theorem of calculus, the Arzelà-Ascoli theorem, the...

(the Green's function of the problem). As a consequence of the Arzelà–Ascoli theorem, this integral operator is compact and existence of a sequence of...

tool for showing compact convergence is the Arzelà–Ascoli theorem. There are several versions of this theorem, roughly speaking it states that every sequence...

Thus, Skorokhod space is a Polish space. By an application of the Arzelà–Ascoli theorem, one can show that a sequence ( μ n ) n = 1 , 2 , … {\displaystyle...

{\mathcal {C}}(X)} is not reflexive, nor is it weakly complete. The Arzelà–Ascoli theorem holds: A subset K {\displaystyle K} of C ( X ) {\displaystyle {\mathcal...

compact by the Arzelà–Ascoli theorem. In many physical situations, this assumption about the input set is a reasonable one. The theorem, however, gives...

consequence of the Ascoli-Arzelà theorem. Indeed, let (un) be a bounded sequence in C0,β(Ω). Thanks to the Ascoli-Arzelà theorem we can assume without...

basepoint are naturally homeomorphic. Compactness follows from the Arzelà–Ascoli theorem since the image in C(XN) is equicontinuous and uniformly bounded...

_{f}(\delta )\to 0{\text{ as }}\delta \to 0} . By an application of the Arzelà-Ascoli theorem, one can show that a sequence ( μ n ) n = 1 ∞ {\displaystyle (\mu...

function spaces of Georg Cantor, Vito Volterra, Cesare Arzelà, Jacques Hadamard, Giulio Ascoli and others, Maurice Fréchet introduced the metric space...

bounded subset of C(X). We have shown T(X) is equicontinuous, so the Arzelà–Ascoli theorem implies that T(X) is relatively compact. However, the previous bullet...

compact subset of C; they are even holomorphic for |z| > R. So by the Arzelà–Ascoli theorem, passing to a subsequence if necessary, it can be assumed that both...