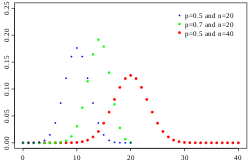
The binomial sum variance inequality states that the variance of the sum of binomially distributed random variables will always be less than or equal to...

Chebyshev–Markov–Stieltjes inequalities Chebyshev's sum inequality Clarkson's inequalities Eilenberg's inequality Fekete–Szegő inequality Fenchel's inequality Friedrichs's...

interval concepts, Michael Short has shown that inequalities on the approximation error between the binomial distribution and the normal distribution can...

probability p, then the variance of the sum will be smaller than the variance of a binomial variable distributed as B(n + m, p). The binomial distribution is...

for example: The binomial distribution B ( n , p ) {\textstyle B(n,p)} is approximately normal with mean n p {\textstyle np} and variance n p ( 1 − p ) {\textstyle...

study of the contributions to sums of squares. Laplace knew how to estimate a variance from a residual (rather than a total) sum of squares. By 1827, Laplace...

the minimum-variance mean (for large normal samples), which is to say the variance of the median will be ~50% greater than the variance of the mean....

unlikely to make a call to that switchboard in that hour. The variance of the binomial distribution is 1 − p times that of the Poisson distribution, so...

distribution, the distribution of a sum of squared standard normal variables; useful e.g. for inference regarding the sample variance of normally distributed samples...

distribution) are considered low-variance, while those with CV > 1 (such as a hyper-exponential distribution) are considered high-variance[citation needed]. Some...

the events happens is no greater than the sum of the probabilities of the individual events. This inequality provides an upper bound on the probability...

\over 12}-{n_{1}n_{2}\sum _{k=1}^{K}(t_{k}^{3}-t_{k}) \over 12n(n-1)}}},\,} where the left side is simply the variance and the right side is the adjustment...

example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical...

finite variance σ 2 {\textstyle \sigma ^{2}} . The sum X 1 + ⋯ + X n {\textstyle X_{1}+\cdots +X_{n}} has mean n μ {\textstyle n\mu } and variance n σ 2...

the sample space. As a result, for random variables with finite variance, the inequality | cov ⁡ ( X , Y ) | ≤ σ 2 ( X ) σ 2 ( Y ) {\displaystyle \left|\operatorname...

{\frac {\operatorname {Var} [X]}{a^{2}}},} where Var is the variance. These inequalities are significant for their nearly complete lack of conditional...

The variance of the sum is equal to the sum of the variances, which is asymptotic to n 2 / log ⁡ n {\displaystyle n^{2}/\log n} . The variance of the...

rule Accuracy and precision Algorithms for calculating variance Chebyshev's inequality An inequality on location and scale parameters Coefficient of variation...

then their sum is distributed according to a binomial distribution with parameters n and p: ∑ k = 1 n X k ∼ B ⁡ ( n , p ) {\displaystyle \sum _{k=1}^{n}X_{k}\sim...

characterizations using the limit and the infinite series can be proved via the binomial theorem. Jacob Bernoulli discovered this constant in 1683, while studying...

For non-normal samples, the variance of the sample variance depends on the kurtosis; for details, please see variance. Pearson's definition of kurtosis...

{1}{\bar {x}}}\right)={\frac {n-2}{\sum _{i}x_{i}}}} This is derived from the mean and variance of the inverse-gamma distribution, Inv-Gamma...

large numbers for any weighted sum of independent Cauchy distributions. This shows that the condition of finite variance in the central limit theorem cannot...

matrix (also known as auto-covariance matrix, dispersion matrix, variance matrix, or variance–covariance matrix) is a square matrix giving the covariance between...

Wald test Bernstein inequalities (probability theory) Binomial regression Binomial proportion confidence interval Chebyshev's inequality Chernoff bound Gauss's...

)=F_{\text{binomial}}(\beta -1;\alpha +\beta -1,1-x)} . The beta distribution may also be reparameterized in terms of its mean μ (0 < μ < 1) and the sum of the...

distribution is strictly subgaussian, any symmetric Binomial distribution is strictly subgaussian. The optimal variance proxy ‖ X ‖ v p 2 {\displaystyle \Vert X\Vert...

. Since the estimator is unbiased, its MSE equals its variance. By rearranging, the inequality tells us that Var ⁡ ( θ ^ ) ≥ 1 I ( θ ) . {\displaystyle...

{y}}{\bar {x}}}={\frac {\sum _{i=1}^{n}y_{i}}{\sum _{i=1}^{n}x_{i}}}} That the ratio is biased can be shown with Jensen's inequality as follows (assuming...

the mean may be derived from the variance of a sum of independent random variables, given the definition of variance and some properties thereof. If x...