algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, the power ⁠...

In mathematics, the binomial series is a generalization of the binomial formula to cases where the exponent is not a positive integer: where α {\displaystyle...

Gaussian binomial coefficients (also called Gaussian coefficients, Gaussian polynomials, or q-binomial coefficients) are q-analogs of the binomial coefficients...

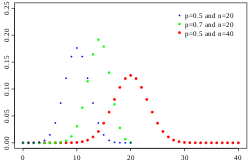
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes...

multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from...

the correct result is given by the binomial theorem. The name "freshman's dream" also sometimes refers to the theorem that says that for a prime number...

mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is...

Abel's binomial theorem, named after Niels Henrik Abel, is a mathematical identity involving sums of binomial coefficients. It states the following: ∑...

approximation can be proven several ways, and is closely related to the binomial theorem. By Bernoulli's inequality, the left-hand side of the approximation...

{\displaystyle n^{k}=\sum _{i=0}^{n-1}\left((i+1)^{k}-i^{k}\right).} Using binomial theorem, this may be rewritten as: n k = ∑ i = 0 n − 1 ( ∑ j = 0 k − 1 ( k...

filters) Binomial series Binomial theorem Binomial transform Binomial type Carlson's theorem Catalan number Fuss–Catalan number Central binomial coefficient...

numbers, in which case we cannot enumerate all irrational numbers. The binomial theorem is closely related to the power set. A k–elements combination from...

limit theorem states that the Poisson distribution may be used as an approximation to the binomial distribution, under certain conditions. The theorem was...

the importance of a general binomial theorem. The argument supporting the claim that Khayyam had a general binomial theorem is based on his ability to...

In probability theory and statistics, the negative binomial distribution, also called a Pascal distribution, is a discrete probability distribution that...

Several theorems related to the triangle were known, including the binomial theorem. Khayyam used a method of finding nth roots based on the binomial expansion...

of binomials Binomial QMF, a perfect-reconstruction orthogonal wavelet decomposition Binomial theorem, a theorem about powers of binomials Binomial type...

A Treatise on the Binomial Theorem is a fictional work of mathematics by the young Professor James Moriarty, the criminal mastermind and archenemy of the...

closely related to the q-exponential. Cauchy binomial theorem is a special case of the q-binomial theorem. ∑ n = 0 N y n q n ( n + 1 ) / 2 [ N n ] q =...

again (4). One can prove Bernoulli's inequality for x ≥ 0 using the binomial theorem. It is true trivially for r = 0, so suppose r is a positive integer...

which is the statement of the theorem for a = k+1. ∎ In order to prove the lemma, we must introduce the binomial theorem, which states that for any positive...

(ax+b)(cx+d)=acx^{2}+(ad+bc)x+bd.} A binomial raised to the nth power, represented as (x + y)n can be expanded by means of the binomial theorem or, equivalently, using...

characterizations using the limit and the infinite series can be proved via the binomial theorem. Jacob Bernoulli discovered this constant in 1683, while studying a...

Moivre–Laplace theorem, which is a special case of the central limit theorem, states that the normal distribution may be used as an approximation to the binomial distribution...

He generalized the binomial theorem to any real number, introduced the Puiseux series, was the first to state Bézout's theorem, classified most of the...

In number theory, Lucas's theorem expresses the remainder of division of the binomial coefficient ( m n ) {\displaystyle {\tbinom {m}{n}}} by a prime...

mathematics, Kummer's theorem is a formula for the exponent of the highest power of a prime number p that divides a given binomial coefficient. In other...

gains recognition at the age of 21 for writing "a treatise upon the Binomial Theorem", which leads to his being awarded the Mathematical Chair at one of...

parentheses denote a binomial coefficient. For example, with p = 7, this says that 1716 is one more than a multiple of 343. The theorem was first proved by...

ai = 0 for all integers i > m and bj = 0 for all integers j > n. By the binomial theorem, ( 1 + x ) m + n = ∑ r = 0 m + n ( m + n r ) x r . {\displaystyle (1+x)^{m+n}=\sum...