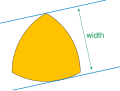
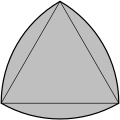
In plane geometry the Blaschke–Lebesgue theorem states that the Reuleaux triangle has the least area of all curves of given constant width. In the form...

ISBN 3889082033 Blaschke's name has been lent as an eponym to a number of mathematical theorems and concepts: Blaschke selection theorem Blaschke–Lebesgue theorem Blaschke...

^{n}} . This follows from the general form of Crofton formula. Blaschke–Lebesgue theorem and isoperimetric inequality, bounding the areas of curves of...

Henri Lebesgue: Blaschke–Lebesgue theorem Cantor–Lebesgue function Borel–Lebesgue theorem Fatou–Lebesgue theorem Lebesgue constant Lebesgue covering dimension...

space Lebesgue–Stieltjes integration Lebesgue–Vitali theorem Blaschke–Lebesgue theorem Borel–Lebesgue theorem Fatou–Lebesgue theorem Riemann–Lebesgue lemma...

The Blaschke selection theorem is a result in topology and convex geometry about sequences of convex sets. Specifically, given a sequence { K n } {\displaystyle...

T\leq {\frac {\sqrt {3}}{4}}(abc)^{2/3}.} Mathematics portal Blaschke–Lebesgue theorem Chaplygin problem: isoperimetric problem is a zero wind speed...

triangle is one of the most extreme curves of constant width. By the Blaschke–Lebesgue theorem, the Reuleaux triangle has the smallest possible area of any curve...

inequality and Barbier's theorem, the circle has the maximum area of any curve of given constant width. The Blaschke–Lebesgue theorem says that the Reuleaux...

Disintegration theorem (measure theory) Dominated convergence theorem (Lebesgue integration) Egorov's theorem (measure theory) Fatou–Lebesgue theorem (real analysis)...

Finding Ellipses: What Blaschke Products, Poncelet’s Theorem, and the Numerical Range Know about Each Other is a mathematics book on "some surprising...

translations allowed, but not rotations) Blaschke selection theorem, which can be used to prove that Lebesgue's universal covering problem has a solution...

Wilhelm Blaschke. He was appointed Professor in Königsberg in 1934, and subsequently held posts in a number of universities until 1974. Sperner's theorem, from...

inequality Barrow's inequality Berger–Kazdan comparison theorem Blaschke–Lebesgue inequality Blaschke–Santaló inequality Bishop–Gromov inequality Bogomolov–Miyaoka–Yau...

the Lp Brunn-Minkowski theory. Blaschke sum – Polytope combining two smaller polytopes Brunn–Minkowski theorem – theorem in geometryPages displaying wikidata...

1918, Vienna) was an Austrian mathematician, known for the Gross star theorem. Wilhelm Gross graduated from the Gymnasium in Linz and then studied from...

{\displaystyle \displaystyle {\varphi (z)=cB(z)e^{-P(z)},}} where |c|=1, B(z) is a Blaschke product B ( z ) = ∏ [ | λ i | λ i λ i − z 1 − λ ¯ i ] m i , {\displaystyle...

subsets of a set X {\displaystyle X} to an abelian semigroup. For example, Lebesgue measure is a valuation on finite unions of convex bodies of R n . {\displaystyle...

exist a smallest convex cover. Its existence follows from the Blaschke selection theorem. It is also not trivial to determine whether a given shape forms...

credits the formulation of this problem to a 1916 publication of Wilhelm Blaschke. Bolker, Ethan D. (1969), "A class of convex bodies", Transactions of the...

legacy. Elsevier. p. 193. ISBN 978-0-444-52728-8. They mention Wilhelm Blaschke's claim in 1959 that "the quaternions were first identified by L. Euler...

Gustav Jacob Jacobi (1827, 1833/34), Michel Chasles (1829), Victor-Amédée Lebesgue (1837), Thomas Weddle (1847), Edmond Bour (1856), Osip Ivanovich Somov...