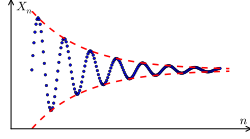
specifically in real analysis, the Bolzano–Weierstrass theorem, named after Bernard Bolzano and Karl Weierstrass, is a fundamental result about convergence...

Weierstrass formalized the definition of the continuity of a function and complex analysis, proved the intermediate value theorem and the Bolzano–Weierstrass...

Stone–Weierstrass theorem The Bolzano–Weierstrass theorem, which ensures compactness of closed and bounded sets in Rn The Weierstrass extreme value theorem...

as the intermediate value theorem, the Bolzano–Weierstrass theorem, the extreme value theorem, and the Heine–Borel theorem. It is usually taken as an...

numbers. The Bolzano–Weierstrass theorem states that every bounded sequence of real numbers has a convergent subsequence. Again, this theorem is equivalent...

infinite subsequence that converges to some point of the space. The Bolzano–Weierstrass theorem states that a subset of Euclidean space is compact in this sequential...

intermediate value theorem (also known as Bolzano's theorem). Today he is mostly remembered for the Bolzano–Weierstrass theorem, which Karl Weierstrass developed...

today as the Bolzano–Weierstrass theorem. The following examples show why the function domain must be closed and bounded in order for the theorem to apply...

In mathematics, the Weierstrass function, named after its discoverer, Karl Weierstrass, is an example of a real-valued function that is continuous everywhere...

Weierstrass. Bolzano–Weierstrass theorem Casorati–Weierstrass theorem Weierstrass method Enneper–Weierstrass parameterization Lindemann–Weierstrass theorem...

opposite sign inside an interval, then it has a root in that interval (Bolzano's theorem). The image of a continuous function over an interval is itself an...

property. All Montel spaces have the Heine–Borel property as well. Bolzano–Weierstrass theorem Raman-Sundström, Manya (August–September 2015). "A Pedagogical...

bounded, the set of points {f(x1)}f∈F is bounded, and hence by the Bolzano–Weierstrass theorem, there is a sequence {fn1} of distinct functions in F such that...

monotone subsequence. (This is a lemma used in the proof of the Bolzano–Weierstrass theorem.) Every infinite bounded sequence in R n {\displaystyle \mathbb...

Arzelà–Ascoli theorem (functional analysis) Baire category theorem (topology, metric spaces) Bing metrization theorem (general topology) Bolzano–Weierstrass theorem...

Banach fixed-point theorem Banach–Tarski paradox Basel problem Bolzano–Weierstrass theorem Brouwer fixed-point theorem Buckingham π theorem (proof in progress)...

below.) The existence of the limit can be proved by the means of Bolzano–Weierstrass theorem in a manner almost identical to the proof of existence of arithmetic–geometric...

convergent sequences should all converge to the extra point. Bolzano–Weierstrass theorem – Bounded sequence in finite-dimensional Euclidean space has...

the Bolzano–Weierstrass theorem, yield one standard proof of the completeness of the real numbers, closely related to both the Bolzano–Weierstrass theorem...

recent. More popular in the 19th and early 20th centuries was the Bolzano-Weierstrass criterion that every bounded infinite sequence admits a convergent...

greatest-lower-bound property The nested interval property The Bolzano-Weierstrass theorem The convergence of Cauchy sequences A typical real analysis university...

supremum (proof below), the convergence of Cauchy sequences and the Bolzano–Weierstrass theorem. This means that one of the four has to be introduced axiomatically...

infinitesimal. It can be proven by bisection method used in proving the Bolzano-Weierstrass theorem, the property (1) of ultrafilters turns out to be crucial. The...

theorem). This fact may be used to prove minimization results for continuous convex functionals, in the same way that the Bolzano–Weierstrass theorem...

sequence of real numbers has a limit).theorem III.2.2 The Bolzano–Weierstrass theorem.theorem III.2.2 Ascoli's theorem: every bounded equicontinuous sequence...

also an interval Heine–Borel theorem – sometimes used as the defining property of compactness Bolzano–Weierstrass theorem – states that each bounded sequence...

would like to show them to converge to a limiting point with the Bolzano-Weierstrass theorem. To do so, we construe these two interval sequences as a single...

level set of a minimization problems is not compact, so that the Bolzano–Weierstrass theorem cannot be applied. The principle relies on the completeness of...

mathematical theorems. For example, the intermediate value theorem for functions from the reals to the reals is provable in RCA0, while the Bolzano–Weierstrass theorem...

continuity were first given by Bolzano in the 1830s, but the work wasn't published until the 1930s. Like Bolzano, Karl Weierstrass denied continuity of a function...