mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is...

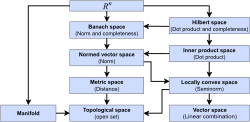
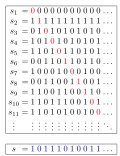
topology, a Cantor space is a topological space homeomorphic to the Cantor ternary set (equipped with its subspace topology). The Cantor set is naturally...

the Cantor space 2 N {\displaystyle \mathbf {2} ^{\mathbb {N} }} . We start with a continuous function h {\displaystyle h} from the Cantor space C {\displaystyle...

quantifiers can naturally be viewed as quantifying over Cantor space. A subset of Cantor space is assigned the classification Σ n 0 {\displaystyle \Sigma...

quantifiers can naturally be viewed as quantifying over Cantor space. A subset of Cantor space is assigned the classification Σ n 1 {\displaystyle \Sigma...

Polish spaces are a particularly convenient setting for descriptive set theory. Examples of such spaces include the Cantor space and Baire space. Hausdorff...

totally disconnected space, these are the only connected subsets. An important example of a totally disconnected space is the Cantor set, which is homeomorphic...

characterize Cantor cubes; any space satisfying the properties is homeomorphic to a Cantor cube. In fact, every AE(0) space is the continuous image of a Cantor cube...

any separable Banach space, the Cantor space, and the Baire space. Additionally, some spaces that are not complete metric spaces in the usual metric may...

connected space or Cantor connected space is a uniform space U such that every uniformly continuous function from U to a discrete uniform space is constant...

interpreted as the measure of a certain subset of Cantor space under the usual probability measure on Cantor space. It is from this interpretation that halting...

the discrete space { 0 , 1 } {\displaystyle \{0,1\}} is homeomorphic to the Cantor set; and in fact uniformly homeomorphic to the Cantor set if we use...

Bergman space Berkovich space Besov space Borel space Calabi-Yau space Cantor space Cauchy space Cellular space Chu space Closure space Conformal space Complex...

Every Polish space. BCT2 shows that the following are Baire spaces: Every compact Hausdorff space; for example, the Cantor set (or Cantor space). Every manifold...

Antoine's necklace is a topological embedding of the Cantor set in 3-dimensional Euclidean space, whose complement is not simply connected. It also serves...

Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6...

Quotient space Unit interval Continuum Extended real number line Long line (topology) Sierpinski space Cantor set, Cantor space, Cantor cube Space-filling...

{\displaystyle T(b_{0},b_{1},b_{2},\dots )=(b_{1},b_{2},\dots )} defined on the Cantor space Ω = { 0 , 1 } N {\displaystyle \Omega =\{0,1\}^{\mathbb {N} }} . That...

{N}}} , the Cantor space C {\displaystyle {\mathcal {C}}} , and the Hilbert cube I N {\displaystyle I^{\mathbb {N} }} . The class of Polish spaces has several...

in general: for instance Cantor space is totally disconnected but not discrete. Let X {\displaystyle X} be a topological space, and let x {\displaystyle...

for all closed subsets of Polish spaces, in which case the theorem is known as the Cantor–Bendixson theorem. Cantor also showed that every non-empty perfect...

the concept of a Baire space, which is a certain kind of topological space.) The Baire space can be contrasted with Cantor space, the set of infinite sequences...

Rham curve is a continuous fractal curve obtained as the image of the Cantor space, or, equivalently, from the base-two expansion of the real numbers in...

Cantor's diagonal argument (among various similar names) is a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence...

open set in Cantor space. The product measure μ(Cw) of the cylinder generated by w is defined to be 2−|w|. Every open subset of Cantor space is the union...

Baire space or Cantor space or the real line. There is a close relationship between the relativized analytical hierarchy on subsets of Baire space (denoted...

examples in general topology, a field of mathematics. Alexandrov topology Cantor space Co-kappa topology Cocountable topology Cofinite topology Compact-open...

Cantor distribution Cantor function Cantor medal, German mathematics prize named after Georg Cantor Cantor set Cantor space Cantor's theorem (disambiguation)...

cartesian product of X with the Baire space. A is the projection of a Gδ set in the cartesian product of X with the Cantor space 2ω. An alternative characterization...

inverse image f − 1 [ 0 ] {\displaystyle f^{-1}[0]} as a subset of the Cantor space { 0 , 1 } ω {\displaystyle \{0,1\}^{\omega }} , then f − 1 [ 0 ] {\displaystyle...