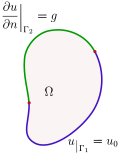
In mathematics, a Cauchy (French: [koʃi]) boundary condition augments an ordinary differential equation or a partial differential equation with conditions...

boundary condition specifies the values of the solution itself (as opposed to its derivative) on the boundary, whereas the Cauchy boundary condition,...

the Cauchy boundary condition and the mixed boundary condition. The latter is a combination of the Dirichlet and Neumann conditions. Neumann boundary condition...

study this problem. Dirichlet boundary condition Neumann boundary condition Cauchy boundary condition Robin boundary condition Obviously, it is not at all...

the domain. A Cauchy problem can be an initial value problem or a boundary value problem (for this case see also Cauchy boundary condition). It is named...

the boundary has the form of a curve or surface that gives a value to the normal derivative and the variable itself then it is a Cauchy boundary condition...

In physics, a Cauchy horizon is a light-like boundary of the domain of validity of a Cauchy problem (a particular boundary value problem of the theory...

boundary condition Cauchy's convergence test Cauchy (crater) Cauchy determinant Cauchy distribution Cauchy's equation Cauchy–Euler equation Cauchy's functional...

mathematics, the Robin boundary condition (/ˈrɒbɪn/ ROB-in, French: [ʁɔbɛ̃]), or third type boundary condition, is a type of boundary condition, named after Victor...

Augustin-Louis Cauchy include: Bolzano–Cauchy theorem Cauchy boundary condition Cauchy completion Cauchy-continuous function Cauchy–Davenport theorem Cauchy distribution...

its values on the boundary of the disk, and it provides integral formulas for all derivatives of a holomorphic function. Cauchy's formula shows that...

a Cauchy surface is usually interpreted as defining an "instant of time". In the mathematics of general relativity, Cauchy surfaces provide boundary conditions...

In complex analysis, the residue theorem, sometimes called Cauchy's residue theorem, is a powerful tool to evaluate line integrals of analytic functions...

continuum mechanics, the Cauchy stress tensor (symbol σ {\displaystyle {\boldsymbol {\sigma }}} , named after Augustin-Louis Cauchy), also called true stress...

In mathematics, a CR manifold, or Cauchy–Riemann manifold, is a differentiable manifold together with a geometric structure modeled on that of a real hypersurface...

In mathematics, the Cauchy–Kovalevskaya theorem (also written as the Cauchy–Kowalevski theorem) is the main local existence and uniqueness theorem for...

interior) is a 3-manifold with boundary. Its boundary is a sphere, a 2-manifold. In technical language, a manifold with boundary is a space containing both...

a unique solution. It is also known as Picard's existence theorem, the Cauchy–Lipschitz theorem, or the existence and uniqueness theorem. The theorem...

y)+iv(x,y),} then the necessary condition that f(z) be analytic is that u and v be differentiable and that the Cauchy–Riemann equations be satisfied:...

intersect the partial Cauchy surface. If the Cauchy surface were compact, i.e. space is compact, the null geodesic generators of the boundary can intersect everywhere...

three-dimensional Cauchy surface, and furthermore that any two Cauchy surfaces for M are diffeomorphic. In particular, M is diffeomorphic to the product of a Cauchy surface...

Laplacian vector field. A Laplacian vector field in the plane satisfies the Cauchy–Riemann equations: it is holomorphic. Suppose the curl of u {\displaystyle...

differential equations Boundary condition Boundary value problem Dirichlet problem, Dirichlet boundary condition Neumann boundary condition Stefan problem Wiener–Hopf...

the boundary. In the obstacle problem, we impose an additional constraint: we minimize the functional E {\displaystyle E} subject to the condition u ≤...

equations associated with Cauchy initial value problems. Cauchy–Kowalevski–Kashiwara theorem is a wide generalization of the Cauchy–Kowalevski theorem for...

{\displaystyle \partial D} be its boundary. Then D ∪ ∂ D ⊂ U {\displaystyle D\cup \partial D\subset U} . Using Cauchy's differentiation formula to calculate...

The two main singular integral operators, the Hilbert transform and the Cauchy transform, can be defined for any smooth Jordan curve in the complex plane...

There are many results on this topic. For example, the Cauchy–Kowalevski theorem for Cauchy initial value problems essentially states that if the terms...

The insight of Bolzano and Cauchy was to define a general notion of continuity (in terms of infinitesimals in Cauchy's case and using real inequalities...

\forall t\in [0,\infty )} . The Cauchy problem consists in finding a solution of the equation, satisfying the initial condition u ( 0 ) = u 0 ∈ D ( A ) ∩ D...