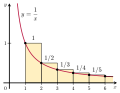
The Cauchy formula for repeated integration, named after Augustin-Louis Cauchy, allows one to compress n antiderivatives of a function into a single integral...

triple integrals. For repeated antidifferentiation of a single-variable function, see the Cauchy formula for repeated integration. Just as the definite...

integrand (so that other integration techniques, such as integration by substitution, may be used) Cauchy formula for repeated integration (to calculate the...

equation Cauchy horizon Cauchy formula for repeated integration Cauchy–Frobenius lemma Cauchy–Hadamard theorem Cauchy–Kovalevskaya theorem Cauchy momentum...

is the most often used. It is a generalization of the Cauchy formula for repeated integration to arbitrary order. Here, n = ⌈ q ⌉ {\displaystyle n=\lceil...

from Cauchy formula for repeated integration. For a function f continuous on the interval [a,x], the Cauchy formula for n-fold repeated integration states...

Log-Cauchy distribution Wrapped Cauchy distribution Cauchy–Euler equation Cauchy's functional equation Cauchy filter Cauchy formula for repeated integration...

The Cauchy distribution, named after Augustin-Louis Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as...

zero even at infinity, methods based on partial integration and the Cauchy formula for repeated integration can be used to compute closed-form solutions...

calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of...

In mathematics, an Euler–Cauchy equation, or Cauchy–Euler equation, or simply Euler's equation, is a linear homogeneous ordinary differential equation...

\end{aligned}}} and this can be extended arbitrarily. The Cauchy formula for repeated integration, namely ( J n f ) ( x ) = 1 ( n − 1 ) ! ∫ 0 x ( x − t )...

{t}{2n+1}}\left({\frac {t^{n}}{n!}}\right)^{2}} . This is given by the Cauchy formula for repeated integration. Every continuous martingale (starting at the origin) is...

less a synonym for "numerical integration", especially as applied to one-dimensional integrals. Some authors refer to numerical integration over more than...

developed by Colin Maclaurin and Augustin-Louis Cauchy and is sometimes known as the Maclaurin–Cauchy test. Consider an integer N and a function f defined...

some powerful results regarding Taylor expansions. For example, using Cauchy's integral formula for any positively oriented Jordan curve γ {\textstyle...

b(x)=x} , which is another common situation (for example, in the proof of Cauchy's repeated integration formula), the Leibniz integral rule becomes: d d x...

e^{z}=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}} , computed by Cauchy's integral formula as 1 n ! = 1 2 π i ∮ | z | = r e z z n + 1 d z . {\displaystyle...

only for | r | < 1. {\displaystyle |r|<1.} However, both the ratio test and the Cauchy–Hadamard theorem are proven using the geometric series formula as...

in Cauchy's 1823 Résumé des Leçons données a L’École Royale Polytechnique sur Le Calcul Infinitesimal. The simplest form of the chain rule is for real-valued...

because integration is the inverse operation of differentiation, Lagrange's notation for higher order derivatives extends to integrals as well. Repeated integrals...

problem of integration into a problem in algebra. It is based on the form of the function being integrated and on methods for integrating rational functions...

Euler–Maclaurin summation formula and integral transforms such as the Laplace and Mellin transforms. Repeated integration by parts will often lead to...

useful properties, such as repeated differentiability, expressibility as power series, and satisfying the Cauchy integral formula. In real analysis, it is...

in a plane perpendicular to that axis. This formula does not a priori define a legitimate vector field, for the individual circulation densities with respect...

and taking the limit yields a term which is bounded from above by the Cauchy–Schwarz inequality | ∇ v f ( x ) | = | ∇ f ⋅ v | ≤ | ∇ f | | v | = | ∇ f...

equation solutions. This example covers only the case for real, separate eigenvalues. Real, repeated eigenvalues require solving the coefficient matrix with...

arbitrary choice of the constant of integration. Using operator algebra avoids cluttering the formula with repeated copies of the function to be operated...

procedure for solving ordinary differential equations (ODEs) with a given initial value. It is the most basic explicit method for numerical integration of ordinary...

Each root for the variable is the value which would give an undefined value to the expression since we do not divide by zero. General formula for a cubic...