In constructive mathematics, Church's thesis C T {\displaystyle {\mathrm {CT} }} is the principle stating that all total functions are computable functions...
15 KB (2,657 words) - 14:12, 21 April 2024
the Church–Turing thesis (also known as computability thesis, the Turing–Church thesis, the Church–Turing conjecture, Church's thesis, Church's conjecture...
58 KB (6,849 words) - 00:41, 20 June 2025
Markov's principle (category Constructivism (mathematics))
Constructive analysis Church's thesis (constructive mathematics) Limited principle of omniscience Margenstern, Maurice (1995). "L'école constructive de...
9 KB (1,370 words) - 20:51, 17 February 2025
In mathematics, constructive analysis is mathematical analysis done according to some principles of constructive mathematics. The name of the subject...
31 KB (4,959 words) - 13:21, 25 May 2025
Axiom schema of predicative separation Constructive mathematics Constructive analysis Constructive Church's thesis rule and principle Computable set Diaconescu's...
213 KB (35,228 words) - 09:33, 13 June 2025
Indecomposability (intuitionistic logic) (redirect from Indecomposability (constructive mathematics))
1928 using intuitionistic principles, and can also be proven using Church's thesis. The analogous property in classical analysis is the fact that every...
4 KB (353 words) - 16:14, 3 November 2024
Hilbert and Bernays, the constructive recursive mathematics of mathematicians Shanin and Markov, and Bishop's program of constructive analysis. Constructivism...
27 KB (2,770 words) - 20:40, 25 June 2025
computable Church's thesis (constructive mathematics), an axiom in constructive mathematics which states that all total functions are computable Church (disambiguation)...
617 bytes (104 words) - 03:05, 9 March 2023
In mathematics, an expression is a written arrangement of symbols following the context-dependent, syntactic conventions of mathematical notation. Symbols...
44 KB (5,463 words) - 12:55, 30 May 2025
Robin, 1978, Church's Thesis and the Principles for Mechanisms, in (Barwise et al. 1980:123-148) George, Alexander (+ed.), 1994, Mathematics and Mind, 216...
61 KB (8,298 words) - 16:15, 11 April 2025
Entscheidungsproblem (redirect from Church's Theorem)
Principles of Mathematical Logic. AMS Chelsea Publishing, Providence, Rhode Island, USA, 1950 Church's paper was presented to the American Mathematical Society...
19 KB (2,642 words) - 21:03, 19 June 2025
In mathematics, and particularly in set theory, category theory, type theory, and the foundations of mathematics, a universe is a collection that contains...
18 KB (2,649 words) - 10:37, 24 June 2025
Mathematical induction is a method for proving that a statement P ( n ) {\displaystyle P(n)} is true for every natural number n {\displaystyle n} , that...
47 KB (6,914 words) - 03:09, 21 June 2025
many adherents, and it was not until Bishop's work in 1967 that constructive mathematics was placed on a sounder footing. One may consider that Hilbert's...
52 KB (6,910 words) - 08:29, 16 June 2025
Setoid (category Equivalence (mathematics))
particularly the proof theory of constructive mathematics based on the Curry–Howard correspondence, one often identifies a mathematical proposition with its set...
5 KB (532 words) - 01:05, 22 February 2025
Proof theory (category Mathematical logic)
corresponding parts, with part D being about "Proof Theory and Constructive Mathematics". Prawitz (1965, p. 98). Girard, Taylor & Lafont 2003. Chaudhuri...
20 KB (2,666 words) - 15:22, 15 March 2025
Gödel's incompleteness theorems (redirect from Bew (mathematical logic))
published by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of mathematics. The theorems are widely, but not universally,...
92 KB (12,173 words) - 02:29, 24 June 2025
Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining...
38 KB (4,782 words) - 10:20, 2 June 2025
to solve the problem by changing of logical framework, such as constructive mathematics and intuitionistic logic. Roughly speaking, the first one consists...
83 KB (10,555 words) - 20:05, 9 June 2025
them the infinite can never be completed: In classical mathematics there occur non-constructive or indirect existence proofs, which intuitionists do not...
37 KB (5,624 words) - 22:05, 13 June 2025
In mathematics, Church encoding is a means of representing data and operators in the lambda calculus. The Church numerals are a representation of the...
48 KB (8,556 words) - 17:17, 6 June 2025
In mathematics, a structure on a set (or on some sets) refers to providing or endowing it (or them) with certain additional features (e.g. an operation...
6 KB (650 words) - 10:42, 27 June 2025
"Turing's Thesis", asserting the identity of computability in general with computability by Turing machines, as an equivalent form of Church's Thesis. 1954...
8 KB (948 words) - 20:52, 17 February 2025
constructive methods and algorithms to find numerical approximations (as opposed to symbolic manipulations) of solutions to problems in mathematical analysis...
68 KB (7,792 words) - 22:33, 26 June 2025
halting problem. In response, Tegmark notes: sec. V.E that a constructive mathematics formalized measure of free parameter variations of physical dimensions...
19 KB (2,308 words) - 08:01, 27 June 2025
set theory model theory recursion theory, and proof theory and constructive mathematics (considered as parts of a single area). Additionally, sometimes...
69 KB (8,370 words) - 19:12, 10 June 2025
(1903–1979), was also a notable mathematician, making contributions to constructive mathematics and recursive function theory. Andrey Markov was born on 14 June...
10 KB (1,072 words) - 21:36, 10 June 2025
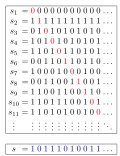
Cantor's diagonal argument (category Theorems in the foundations of mathematics)
{\displaystyle S} and a subset of S {\displaystyle S} . Also in constructive mathematics, there is no surjection from the full domain N {\displaystyle {\mathbb...
27 KB (2,751 words) - 02:16, 12 April 2025
Stratification has several usages in mathematics. In mathematical logic, stratification is any consistent assignment of numbers to predicate symbols guaranteeing...
5 KB (820 words) - 05:59, 26 September 2024
Computable function (section Church–Turing thesis)
model are computable for the above four models of computation. The Church–Turing thesis is the unprovable assertion that every notion of computability that...
24 KB (3,362 words) - 23:24, 22 May 2025