algorithm for matrix multiplication? More unsolved problems in computer science In theoretical computer science, the computational complexity of matrix multiplication...

computational complexity of matrix multiplication) remains unknown. As of April 2024[update], the best announced bound on the asymptotic complexity of...

linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the...

complexity of the chosen multiplication algorithm. This table lists the complexity of mathematical operations on integers. On stronger computational models...

for matrix multiplication. It is faster than the standard matrix multiplication algorithm for large matrices, with a better asymptotic complexity, although...

computational complexity or simply complexity of an algorithm is the amount of resources required to run it. Particular focus is given to computation...

solves 48-year-old multiplication problem". UNSW. Retrieved 2019-04-18. Arora, Sanjeev; Barak, Boaz (2009). Computational Complexity: A Modern Approach...

the (multiplicative) inverse of A, denoted by A−1. Matrix inversion is the process of finding the matrix which when multiplied by the original matrix gives...

greatest lower bound for the exponent of the computational complexity of matrix multiplication. 4.  Written as a function of another function, it is used for...

of simple arithmetic operations needed to compute the product, that is, the computational complexity. The straightforward multiplication of a matrix that...

analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions...

overall computational complexity of the algorithm. The multiplication sub-operations can then be computed recursively using Toom–Cook multiplication again...

S2CID 121761517 Goldreich, O.; Tal, A. (2018), "Matrix rigidity of random Toeplitz matrices", Computational Complexity, 27 (2): 305–350, doi:10.1007/s00037-016-0144-9...

are referred to as matrix norms. Matrix norms differ from vector norms in that they must also interact with matrix multiplication. Given a field   K  ...

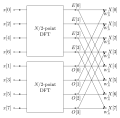
by factorizing the DFT matrix into a product of sparse (mostly zero) factors. As a result, it manages to reduce the complexity of computing the DFT from...

transformation), then the inverse of the example matrix should be used, which coincides with its transpose. Since matrix multiplication has no effect on the zero...

operations such as multiplication falls significantly, often leading to huge savings in terms of calculation time and complexity. As sparse matrices...

must rely on iterative estimation of some parameters. This means that both the computation time and the complexity of the operations involved may vary...

Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division. The...

the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly...

avoids the overhead induced by the non-linearity of the computational complexity of integer multiplication).[citation needed] For coefficients in a finite...

"Triangular Factorization and Inversion by Fast Matrix Multiplication". Mathematics of Computation. 28 (125): 231–236. doi:10.1090/S0025-5718-1974-0331751-8...

unsolved problems in computer science In computational complexity theory, the online matrix-vector multiplication problem (OMv) asks an online algorithm...

research in computational complexity theory and algorithms. She is currently the Steven and Renee Finn Career Development Associate Professor of Electrical...

matrices offer a major advantage: the results of matrix arithmetic operations like matrix multiplication, factorization or inversion can be approximated...

Distance set Hollow matrix Min-plus matrix multiplication Weyenberg, G., & Yoshida, R. (2015). Reconstructing the phylogeny: Computational methods. In Algebraic...

column lengths of both matrices are n) and O ( n ) {\displaystyle O(n)} for multiplication and addition respectively. // Matrix multiplication for (i = 0;...

executes short FFT operations on the columns and rows of the matrix, with a correction multiplication by "twiddle factors" in between. The algorithm got...

unsolved problems in computer science In computational complexity theory, the class NC (for "Nick's Class") is the set of decision problems decidable in polylogarithmic...

encoded position, and find the encoding of the position n-steps-ahead or n-steps-behind, by a matrix multiplication. By taking a linear sum, any convolution...