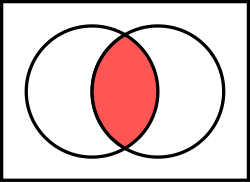
Conjunction introduction (often abbreviated simply as conjunction and also called and introduction or adjunction) is a valid rule of inference of propositional...

fits the form conjunction introduction: Bob likes apples. Bob likes oranges. Therefore, Bob likes apples and Bob likes oranges. Conjunction elimination...

conjunction, a mathematical operator Conjunction introduction, a rule of inference of propositional logic Conjunction (astronomy), in which two astronomical...

In propositional logic, conjunction elimination (also called and elimination, ∧ elimination, or simplification) is a valid immediate inference, argument...

In grammar, a conjunction (abbreviated CONJ or CNJ) is a part of speech that connects words, phrases, or clauses, which are called its conjuncts. That...

\quad \quad }}} ¬ φ {\displaystyle \lnot \varphi } Adjunction (or Conjunction Introduction) φ {\displaystyle \varphi } ψ     _ {\displaystyle {\underline...

Negation introduction is a rule of inference, or transformation rule, in the field of propositional calculus. Negation introduction states that if a given...

In propositional logic, biconditional introduction is a valid rule of inference. It allows for one to infer a biconditional from two conditional statements...

negation elimination. Further rules include conjunction introduction, conjunction elimination, disjunction introduction, disjunction elimination, constructive...

Disjunction introduction or addition (also called or introduction) is a rule of inference of propositional logic and almost every other deduction system...

19th-century British mathematician. The rules allow the expression of conjunctions and disjunctions purely in terms of each other via negation. The rules...

falsehood of its negation." Double negation elimination and double negation introduction are two valid rules of replacement. They are the inferences that, if...

connectives with explicit proofs. For conjunction, we look at the introduction rule ∧I to discover the form of proofs of conjunction: they must be a pair of proofs...

Implication introduction / elimination (modus ponens) Biconditional introduction / elimination Conjunction introduction / elimination Disjunction introduction /...

Irving M.; Cohen, Carl (2005). Introduction to Logic. Prentice Hall. p. 362. Hurley, Patrick (1991). A Concise Introduction to Logic 4th edition. Wadsworth...

 Distribution of   conjunction   over   disjunction  ( P ∨ ( Q ∧ R ) ) ⇔ ( ( P ∨ Q ) ∧ ( P ∨ R ) )  Distribution of   disjunction   over   conjunction  ( P ∧ (...

edu. Retrieved 6 March 2020. Herbert B. Enderton, 2001, A Mathematical Introduction to Logic Second Edition, Harcourt Academic Press, Burlington MA, ISBN 978-0-12-238452-3...

2011). A Concise Introduction to Logic. Cengage Learning. ISBN 978-0-8400-3417-5. Copi, Irving M.; Cohen, Carl (2005). Introduction to Logic. Prentice...

it: "Modus ponendo tollens is the principle that, if the negation of a conjunction holds and also one of its conjuncts, then the negation of its other conjunct...

not a free variable of ψ {\displaystyle \psi } . Conjunction introduction and elimination introduction: α → ( β → α ∧ β ) {\displaystyle \alpha \to (\beta...

McMahon (Nov 2010). Introduction to Logic. Pearson Education. ISBN 978-0205820375.[page needed] Hurley, Patrick. A Concise Introduction to Logic. Wadsworth...

reductio ad absurdum (RAA) in the following way: Hurley, Patrick. A Concise Introduction to Logic With Ilrn Printed Access Card. Wadsworth Pub Co, 2008. Page...

is therefore critical to a statement's trueness or falseness. Logical conjunctions are used to restrict the domain of discourse to fulfill a given predicate...

long as). French grammar "French Conjunctions". Lawless French. Retrieved 5 May 2023. "Introduction to French Conjunctions". ThoughtCo. Retrieved 5 May 2023...

((P\lor Q)\lor R)\leftrightarrow (P\lor (Q\lor R))} Associativity of conjunction ( ( P ∧ Q ) ∧ R ) ↔ ( P ∧ ( Q ∧ R ) ) {\displaystyle ((P\land Q)\land...

replacement. The rules are used to eliminate redundancy in disjunctions and conjunctions when they occur in logical proofs. They are: The principle of idempotency...

propositions by logical connectives representing the truth functions of conjunction, disjunction, implication, biconditional, and negation. Some sources...

of the transfer of disjunctive operator. Hurley, Patrick. A Concise Introduction to Logic With Ilrn Printed Access Card. Wadsworth Pub Co, 2008. Page...

propositional calculus systems with implication and negation (i.e. without the conjunction symbol), is the following: (HS1) ( Q → R ) → ( ( P → Q ) → ( P → R )...

that permits conjunctions or disjunctions with less than κ constituents is known as Lκω. For example, Lω1ω permits countable conjunctions and disjunctions...