In knot theory, Conway notation, invented by John Horton Conway, is a way of describing knots that makes many of their properties clear. It composes a...

mathematical field of knot theory, the Dowker–Thistlethwaite (DT) notation or code, for a knot is a sequence of even integers. The notation is named after Clifford...

of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot. The...

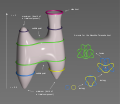
Dowker–Thistlethwaite notation. The Conway notation for knots and links, named after John Horton Conway, is based on the theory of tangles (Conway 1970). The advantage...

Conway FRS (26 December 1937 – 11 April 2020) was an English mathematician. He was active in the theory of finite groups, knot theory, number theory,...

In knot theory, the cinquefoil knot, also known as Solomon's seal knot or the pentafoil knot, is one of two knots with crossing number five, the other...

In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining the two...

In knot theory, the three-twist knot is the twist knot with three-half twists. It is listed as the 52 knot in the Alexander-Briggs notation, and is one...

Computation. 105 (2–3): 271–289. doi:10.1016/S0096-3003(98)10106-6. MR 1710214. See p. 274 Conway notation (knot theory) Dowker–Thistlethwaite notation v t e...

Conway notation may refer to the following notations created by John Horton Conway: Conway chained arrow notation Conway notation (knot theory) Conway...

specifically in knot theory, the Conway knot (or Conway's knot) is a particular knot with 11 crossings, named after John Horton Conway. It is related by...

In knot theory, a figure-eight knot (also called Listing's knot) is the unique knot with a crossing number of four. This makes it the knot with the third-smallest...

In knot theory, the stevedore knot is one of three prime knots with crossing number six, the others being the 62 knot and the 63 knot. The stevedore knot...

standard diagram for this link. In The Knot Atlas, the Borromean rings are denoted with the code "L6a4"; the notation means that this is a link with six crossings...

this relation gives a Laurent polynomial in t1/2. See knot theory for an example computing the Conway polynomial of the trefoil. Using pseudo-holomorphic...

by Conway in 1968 Conway knot – a curious knot having the same Alexander polynomial and Conway polynomial as the unknot Conway notation (knot theory) –...

closures of rational tangles. One motivation for Conway's study of tangles was to provide a notation for knots more systematic than the traditional enumeration...

In knot theory, a prime knot or prime link is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot...

In the mathematical theory of knots, the unknot, not knot, or trivial knot, is the least knotted of all knots. Intuitively, the unknot is a closed loop...

Horton Conway) is a topologically but not smoothly slice knot. On the other hand, the Kinoshita-Terasaka knot, a so-called ′mutant′ of the Conway knot, is...

embedding of a tame knot from the 3-sphere. Notation used in knot theory: Conway notation Dowker–Thistlethwaite notation (DT notation) Gauss code (see also...

In knot theory, the 71 knot, also known as the septoil knot, the septafoil knot, or the (7, 2)-torus knot, is one of seven prime knots with crossing number...

In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies...

In the mathematical theory of knots, a knot is tame if it can be "thickened", that is, if there exists an extension to an embedding of the solid torus...

In mathematical knot theory, a Conway sphere, named after John Horton Conway, is a 2-sphere intersecting a given knot or link in a 3-manifold transversely...

The Knot Atlas is a website, an encyclopedia rather than atlas, dedicated to knot theory. It and its predecessor were created by mathematician Dror Bar-Natan...

In mathematical knot theory, 74 is the name of a 7-crossing knot which can be visually depicted in a highly-symmetric form, and so appears in the symbolism...

as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is...

schemes. Conway knot 11n34 Kinoshita–Terasaka knot 11n42 List of knots List of mathematical knots and links Knot tabulation (−2,3,7) pretzel knot Originally...

classified as a link, and is not a true knot according to the definitions of mathematical knot theory. The Solomon's knot consists of two closed loops, which...