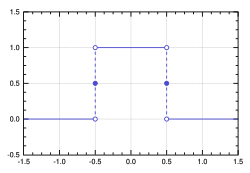
mathematical analysis, the Dirac delta function (or δ distribution), also known as the unit impulse, is a generalized function on the real numbers, whose...

}\delta (t-kT)} for some given period T {\displaystyle T} . Here t is a real variable and the sum extends over all integers k. The Dirac delta function...

continuous-time systems the Dirac delta function is often confused for both the Kronecker delta function and the unit sample function. The Dirac delta is defined as:...

quantum mechanics the delta potential is a potential well mathematically described by the Dirac delta function - a generalized function. Qualitatively, it...

function contains all frequencies (see the Fourier transform of the Dirac delta function, showing infinite frequency bandwidth that the Dirac delta function...

as points with non-zero charge). The Dirac delta function, or δ function, is (informally) a generalized function on the real number line that is zero...

integral of the Dirac delta function. This is sometimes written as H ( x ) := ∫ − ∞ x δ ( s ) d s {\displaystyle H(x):=\int _{-\infty }^{x}\delta (s)\,ds} although...

of formalizing the idea of the Dirac delta function, an important tool in physics and other technical fields. A Dirac measure is a measure δx on a set...

{\displaystyle \delta (t)} is δ ( f ) = 1 , {\displaystyle \delta (f)=1,} means that the frequency spectrum of the Dirac delta function is infinitely broad...

Green's function G {\displaystyle G} is the solution of the equation L G = δ {\displaystyle LG=\delta } , where δ {\displaystyle \delta } is Dirac's delta function;...

1920s and 1930s further basic steps were taken. The Dirac delta function was boldly defined by Paul Dirac (an aspect of his scientific formalism); this was...

continuity in his Cours d'Analyse, and in defining an early form of a Dirac delta function. As Cantor and Dedekind were developing more abstract versions of...

on the indicator function of some domain D. It is a generalisation of the derivative (or "prime function") of the Dirac delta function to higher dimensions;...

potentials that are not functions but are distributions, such as the Dirac delta function. It is easy to visualize a sequence of functions meeting the requirement...

career, Dirac made numerous important contributions to mathematical subjects, including the Dirac delta function, Dirac algebra and the Dirac operator...

The Kronecker delta in mathematics. The central difference for a function. The degree of a vertex in graph theory. The Dirac delta function in mathematics...

A Dirac delta function or simply delta function is a generalized function on the real number line denoted by δ that is zero everywhere except at zero...

distribution becomes a one-point degenerate distribution with a Dirac delta function spike at the right end, x = 1, with probability 1, and zero probability...

arguments. The integral of the Dirac delta function. Sawtooth wave Square wave Triangle wave Rectangular function Floor function: Largest integer less than...

relatively simple applications use the Dirac delta function, which can be treated formally as if it were a function, but the justification requires a mathematically...

non-existent Dirac delta function). However, there are RKHSs in which the norm is an L2-norm, such as the space of band-limited functions (see the example...

the step response to a step input, or the impulse response to a Dirac delta function input. In the frequency domain (for example, looking at the Fourier...

N_{\ell }} is arbitrarily close to this upper bound. Note that the Dirac delta function potential attains this limit. After the first proof of this inequality...

in distribution theory, the derivative of the signum function is two times the Dirac delta function. This can be demonstrated using the identity sgn ⁡ x...

estimated wavelet to a Dirac delta function (i.e., a spike). The result may be seen as a series of scaled, shifted delta functions (although this is not...

singular, such as the Dirac delta function. A function f {\displaystyle f} is normally thought of as acting on the points in the function domain by "sending"...

magnetic field is proportional to the Dirac delta function at the origin. We must define one set of functions for the vector potential on the "northern...

step function is equal to the Dirac delta function, i.e. d H ( x ) d x = δ ( x ) {\displaystyle {\frac {\mathrm {d} H(x)}{\mathrm {d} x}}=\delta (x)}...

of distributions or generalized functions, giving a well-defined meaning to objects such as the Dirac delta function. For several years he taught at the...

introduction of several component wave functions in Pauli's phenomenological theory of spin. The wave functions in the Dirac theory are vectors of four complex...