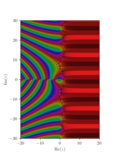
In mathematics, the Dirichlet function is the indicator function 1 Q {\displaystyle \mathbf {1} _{\mathbb {Q} }} of the set of rational numbers Q {\displaystyle...

In mathematics, a Dirichlet L {\displaystyle L} -series is a function of the form L ( s , χ ) = ∑ n = 1 ∞ χ ( n ) n s . {\displaystyle L(s,\chi )=\sum...

mathematics, the Dirichlet beta function (also known as the Catalan beta function) is a special function, closely related to the Riemann zeta function. It is a...

in the area of analytic number theory, the Dirichlet eta function is defined by the following Dirichlet series, which converges for any complex number...

In mathematics, Dirichlet convolution (or divisor convolution) is a binary operation defined for arithmetic functions; it is important in number theory...

Johann Peter Gustav Lejeune Dirichlet (/ˌdɪərɪˈkleɪ/; German: [ləˈʒœn diʁiˈkleː]; 13 February 1805 – 5 May 1859) was a German mathematician. In number...

generating functions, including ordinary generating functions, exponential generating functions, Lambert series, Bell series, and Dirichlet series. Every...

Synchrotron function Riemann zeta function: A special case of Dirichlet series. Riemann Xi function Dirichlet eta function: An allied function. Dirichlet beta...

indicator function of the rational numbers, also known as the Dirichlet function. This function is denoted as 1 Q {\displaystyle \mathbf {1} _{\mathbb {Q}...

Sequences. 13: Article 10.7.4. Apostol, T. M. (1997), "Modular Functions and Dirichlet Series in Number Theory", New York: Springer-Verlag 2nd Ed. Ashworth...

Riemann zeta function is a Dirichlet series, as are the Dirichlet L-functions. Specifically, the Riemann zeta function ζ(s) is the Dirichlet series of the...

names: the popcorn function, the raindrop function, the countable cloud function, the modified Dirichlet function, the ruler function (not to be confused...

the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over...

weight function w appearing in the boundary expression is termed a primary variable, and its specification constitutes the essential or Dirichlet boundary...

is a Dirichlet series, usually convergent on a half-plane, that may give rise to an L-function via analytic continuation. The Riemann zeta function is an...

continuous functions, including elementary functions, for example polynomials. However, the graphs of other functions, for example the Dirichlet function, don't...

periodic but possess properties that make them less intuitive. The Dirichlet function, for example, is periodic, with any nonzero rational number serving...

{1} _{A}(x)=\left[\ x\in A\ \right].} For example, the Dirichlet function is the indicator function of the rational numbers as a subset of the real numbers...

In probability and statistics, the Dirichlet distribution (after Peter Gustav Lejeune Dirichlet), often denoted Dir ⁡ ( α ) {\displaystyle \operatorname...

Riemann zeta function, such as Dirichlet series, Dirichlet L-functions and L-functions, are known. The Riemann zeta function ζ(s) is a function of a complex...

In mathematics, the Dirichlet–Jordan test gives sufficient conditions for a complex-valued, periodic function f {\displaystyle f} to be equal to the sum...

Explicit formula (L-function) Riemann–Siegel formula (particular approximate functional equation) "§25.15 Dirichlet -functions on NIST". Weisstein, Eric...

extension of the Dirichlet function takes different values (0 and 1) at these two infinitely close points, and therefore the Dirichlet function is not continuous...

In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there...

a complex-valued arithmetic function χ : Z → C {\displaystyle \chi :\mathbb {Z} \rightarrow \mathbb {C} } is a Dirichlet character of modulus m {\displaystyle...

In mathematics, a Dirichlet problem asks for a function which solves a specified partial differential equation (PDE) in the interior of a given region...

}}\\0&x{\text{ irrational }}\end{cases}}} (a.k.a., the Dirichlet function) has no limit at any x-coordinate. The function f ( x ) = { 1  for  x < 0 2  for  x ≥ 0 {\displaystyle...

multiplication. A function's being odd or even does not imply differentiability, or even continuity. For example, the Dirichlet function is even, but is...

derivative is finite at 0, i.e. this is an essential discontinuity. The Dirichlet function, defined as: f ( x ) = { 1 , if  x  is rational 0 , if  x  is irrational...

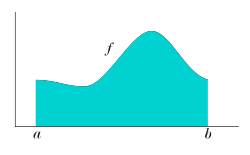
One of which is Dirichlet's principle, representing harmonic functions in the Sobolev space H1(Ω) as the minimizers of the Dirichlet energy integral J...