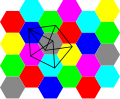
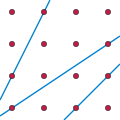
geometry, the Erdős distinct distances problem states that every set of points in the plane has a nearly-linear number of distinct distances. It was posed...

The Erdős–Menger conjecture on disjoint paths in infinite graphs, proved by Ron Aharoni and Eli Berger in 2009. The Erdős distinct distances problem. The...

Willmore conjecture (Fernando Codá Marques and André Neves, 2012) Erdős distinct distances problem (Larry Guth, Nets Hawk Katz, 2011) Heterogeneous tiling conjecture...

The Erdős Distance Problem is a monograph on the Erdős distinct distances problem in discrete geometry: how can one place n {\displaystyle n} points into...

according to the 2015 solution of the Erdős distinct distances problem by Larry Guth and Nets Katz, the distance set of any finite collection of points...

discrepancy problem Erdős distinct distances problem Burr–Erdős conjecture Cameron–Erdős conjecture Erdős–Faber–Lovász conjecture Erdős–Graham conjecture...

analogue of the Erdős distinct distances problem, which states that large finite sets of points must have large numbers of distinct distances. Based on this...

{Z} _{4}^{n}} by Croot, Lev and Pach The Erdős distinct distances problem by Guth and Katz The Joints Problem in 3D by Guth and Katz. Their argument was...

manifolds and, along with Nets Katz, found a solution to the Erdős distinct distances problem. His interests include the Kakeya conjecture and the systolic...

published the results of their collaborative effort to solve the Erdős distinct distances problem, in which they found a "near-optimal" result, proving that...

in turn, enabled Katz and Guth to solve the Erdős distinct distances problem, a 1946 problem of Erdős. Work continues on improvements in Purdy's conjecture...

away a person is from prolific mathematician Paul Erdős and actor Kevin Bacon, respectively—are distances in the graphs whose edges represent mathematical...

which eventually led Guth and Katz to the solution of the Erdős distinct distances problem. (See below.) After graduating from the mathematics program...

Salem–Spencer set Secretary problem Tournament (graph theory) Erdős distinct distances problem Leo Moser at the Mathematics Genealogy Project W. Moser, G...

chromatic number of the plane". By the de Bruijn–Erdős theorem, a result of de Bruijn & Erdős (1951), the problem is equivalent (under the assumption of the...

other model contemporaneously with and independently of Erdős and Rényi. In the model of Erdős and Rényi, all graphs on a fixed vertex set with a fixed...

the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common. Paul Erdős, Chao...

getting wet. The problem was first posed in 1962 by Basil Gordon (although it has sometimes been erroneously attributed to Paul Erdős) and it remains unsolved...

Ngô Bảo Châu. 2010 – Larry Guth and Nets Hawk Katz solve the Erdős distinct distances problem. 2013 – Yitang Zhang proves the first finite bound on gaps...

Ruler Problem". RAIRO - Operations Research. 55 (4). EDP Sciences: 2241–2246. doi:10.1051/ro/2021027. Erdős, Paul; Turán, Pál (1941). "On a problem of Sidon...

Petersen graphs are non-strict unit distance graphs. An unsolved problem of Paul Erdős asks how many edges a unit distance graph on n {\displaystyle n} vertices...

elliptic curve. A negative solution to the Erdős–Ulam problem on dense sets of Euclidean points with rational distances. An effective version of Siegel's theorem...

assumption of the axiom of choice. This is the de Bruijn–Erdős theorem of de Bruijn & Erdős (1951). If a graph admits a full n-coloring for every n ≥...

Her dissertation, Distribution of Distances in Finite Point Sets, is connected to the Erdős distinct distances problem and was supervised by Vera Sós. Vesztergombi's...

[ME] and for the Erdős distinct distances problem, showing that every set of points in the plane has many different pairwise distances.[DD] In 2006, Solymosi...

Research problems in discrete geometry, Berlin: Springer, ISBN 0-387-23815-8 de Bruijn, N. G.; Erdős, P. (1948), "A combinatioral [sic] problem" (PDF),...

to the Erdős distinct distances problem, Palásti studied the existence of point sets for which the i {\displaystyle i} th least frequent distance occurs...

Erdős–Mordell inequality; a stronger variant of it is Barrow's inequality, which replaces the perpendicular distances to the sides with the distances...

four papers with Erdős, giving him an Erdős number of 1, and solved one of Erdős' problems. Guy was intrigued by unsolved problems and wrote two books...

combine a proof of the theorem for finite planar graphs with the De Bruijn–Erdős theorem stating that, if every finite subgraph of an infinite graph is k-colorable...