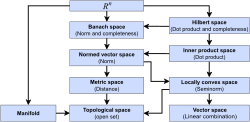
of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X {\displaystyle X}...

topology, a second-countable space, also called a completely separable space, is a topological space whose topology has a countable base. More explicitly...

topological space is called countably compact if every countable open cover has a finite subcover. A topological space X is called countably compact if...

very weak axiom of countability, and all first-countable spaces (notably metric spaces) are sequential. In any topological space ( X , τ ) , {\displaystyle...

the set first-countable space: every point has a countable neighbourhood basis (local base) second-countable space: the topology has a countable base separable...

second-countable space is paracompact. The Sorgenfrey line is paracompact, even though it is neither compact, locally compact, second countable, nor metrizable...

In mathematics, a topological space is called separable if it contains a countable dense subset; that is, there exists a sequence ( x n ) n = 1 ∞ {\displaystyle...

states that every Hausdorff second-countable regular space is metrizable. So, for example, every second-countable manifold is metrizable. (Historical...

the set first-countable space: every point has a countable neighbourhood basis (local base) second-countable space: the topology has a countable base separable...

analytic space Drinfeld's symmetric space Eilenberg–Mac Lane space Euclidean space Fiber space Finsler space First-countable space Fréchet space Function...

two simple requirements: First, the probability of a countable union of mutually exclusive events must be equal to the countable sum of the probabilities...

simplify the literature. For instance, an example of a first-countable space which is not second-countable is counterexample #3, the discrete topology on an...

-convergence in the following way. Let X {\displaystyle X} be a first-countable space and F n : X → R ¯ {\displaystyle F_{n}:X\to {\overline {\mathbb...

Paracompact space Locally compact space Compactly generated space Axiom of countability Sequential space First-countable space Second-countable space Separable...

T_{1}} spaces are characterized by this property. If X {\displaystyle X} is a Fréchet–Urysohn space (which all metric spaces and first-countable spaces are)...

Sequential spaces are CG-2. This includes first countable spaces, Alexandrov-discrete spaces, finite spaces. Every CG-3 space is a T1 space (because given...

true. The spaces for which the two conditions are equivalent are called sequential spaces. All first-countable spaces, including metric spaces, are sequential...

precise sense described herein. In particular, the concept applies to countable families, and thus sequences of functions. Equicontinuity appears in the...

embeddings. Every first-countable space is a Fréchet–Urysohn space. Consequently, every second-countable space, every metrizable space, and every pseudometrizable...

{\displaystyle A} also belongs to A . {\displaystyle A.} In a first-countable space (such as a metric space), it is enough to consider only convergent sequences...

space is a first-countable space if and only if it has order type less than or equal to ω1 (omega-one), that is, if and only if the set is countable or...

metric space is bounded. Every discrete space is first-countable; it is moreover second-countable if and only if it is countable. Every discrete space is...

cluster point, but not conversely. In first-countable spaces, the two concepts coincide. In a topological space, if every subsequence has a subsequential...

Every regular second-countable space is completely normal, and every regular Lindelöf space is normal. Also, all fully normal spaces are normal (even if...

1 ) {\displaystyle [0,\omega _{1})} is first-countable, but neither separable nor second-countable. The space [ 0 , ω 1 ] = ω 1 + 1 {\displaystyle [0...

translation-invariant metric, the second a countable family of seminorms. A topological vector space X {\displaystyle X} is a Fréchet space if and only if it satisfies...

set (also called a meager set or a set of first category) is a subset of a topological space that is a countable union of subsets that are not dense in any...

is sequentially continuous. If X {\displaystyle X} is a first-countable space and countable choice holds, then the converse also holds: any function...

In mathematics, a topological space X {\displaystyle X} is said to be a Baire space if countable unions of closed sets with empty interior also have empty...

second-countable then implies metrizable. Conversely, a compact metric space is second-countable. There are many natural examples of space-filling,...