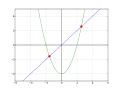
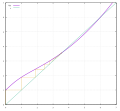
In mathematics, a fixed point (sometimes shortened to fixpoint), also known as an invariant point, is a value that does not change under a given transformation...

Fixed point may refer to: Fixed point (mathematics), a value that does not change under a given transformation Fixed-point arithmetic, a manner of doing...

In mathematics, a fixed-point theorem is a result saying that a function F will have at least one fixed point (a point x for which F(x) = x), under some...

In mathematics, the Lefschetz fixed-point theorem is a formula that counts the fixed points of a continuous mapping from a compact topological space X...

In mathematics, a Hausdorff space X is called a fixed-point space if it obeys a fixed-point theorem, according to which every continuous function f : X...

point (mathematics), a point that is mapped to itself by the function Fixed line telephone, landline All pages with titles beginning with Fixed All pages...

In order theory, a branch of mathematics, the least fixed point (lfp or LFP, sometimes also smallest fixed point) of a function from a partially ordered...

In combinatory logic for computer science, a fixed-point combinator (or fixpoint combinator): p.26  is a higher-order function (i.e., a function which...

In numerical analysis, fixed-point iteration is a method of computing fixed points of a function. More specifically, given a function f {\displaystyle...

In mathematics, the Banach fixed-point theorem (also known as the contraction mapping theorem or contractive mapping theorem or Banach–Caccioppoli theorem)...

Among hundreds of fixed-point theorems, Brouwer's is particularly well known, due in part to its use across numerous fields of mathematics. In its original...

In mathematics, a number of fixed-point theorems in infinite-dimensional spaces generalise the Brouwer fixed-point theorem. They have applications, for...

In mathematics, Lawvere's fixed-point theorem is an important result in category theory. It is a broad abstract generalization of many diagonal arguments...

In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where...

In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry...

In discrete mathematics, a discrete fixed-point is a fixed-point for functions defined on finite sets, typically subsets of the integer grid Z n {\displaystyle...

In mathematical logic, fixed-point logics are extensions of classical predicate logic that have been introduced to express recursion. Their development...

In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation. The point x ~ ∈ R n {\displaystyle...

In mathematics, the fixed-point index is a concept in topological fixed-point theory, and in particular Nielsen theory. The fixed-point index can be thought...

In computing, fixed-point is a method of representing fractional (non-integer) numbers by storing a fixed number of digits of their fractional part. Dollar...

of Mathematics. 5 (2): 311–319. doi:10.2140/pjm.1955.5.311. Cousot, Patrick; Cousot, Radhia (1979). "Constructive versions of tarski's fixed point theorems"...

In functional analysis, a branch of mathematics, the Ryll-Nardzewski fixed-point theorem states that if E {\displaystyle E} is a normed vector space and...

A mathematical object X has the fixed-point property if every suitably well-behaved mapping from X to itself has a fixed point. The term is most commonly...

In mathematics, the Caristi fixed-point theorem (also known as the Caristi–Kirk fixed-point theorem) generalizes the Banach fixed-point theorem for maps...

The Schauder fixed-point theorem is an extension of the Brouwer fixed-point theorem to locally convex topological vector spaces, which may be of infinite...

In the mathematical areas of order and lattice theory, the Kleene fixed-point theorem, named after American mathematician Stephen Cole Kleene, states the...

In mathematics, the Atiyah–Bott fixed-point theorem, proven by Michael Atiyah and Raoul Bott in the 1960s, is a general form of the Lefschetz fixed-point...

In mathematical analysis, the Kakutani fixed-point theorem is a fixed-point theorem for set-valued functions. It provides sufficient conditions for a set-valued...

In mathematics, the Borel fixed-point theorem is a fixed-point theorem in algebraic geometry generalizing the Lie–Kolchin theorem. The result was proved...

fixed points in a n-dimensional space. Mathematically, a rotation is a map. All rotations about a fixed point form a group under composition called the...