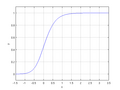
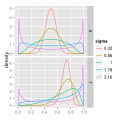
The generalized logistic function or curve is an extension of the logistic or sigmoid functions. Originally developed for growth modelling, it allows...

{erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt} Generalised logistic function f ( x ) = ( 1 + e − x ) − α , α > 0 {\displaystyle...

function in which both asymptotes are approached by the curve symmetrically. It is a special case of the generalised logistic function. The function was...

special case of the generalised logistic function. The growth curve is used to model mean length from age in animals. The function is commonly applied...

requirements of crops. He first described the general form of the generalised logistic function in 1959. Richards was born at Burton-on-Trent, the third child...

this setup are logistic regression models (or logit models). Alternatively, the inverse of any continuous cumulative distribution function (CDF) can be...

A likelihood function (often simply called the likelihood) measures how well a statistical model explains observed data by calculating the probability...

GEV-distributed variables follows a logistic distribution, of which the logit function is the quantile function. The type-I GEV distribution thus plays...

Characterizations of the exponential function Exponential growth Exponentiation Generalised logistic function Logistic distribution SETAR (model) Chan, K...

random variable with a normal distribution, and t is the standard logistic function, then X = t(Y) has a logit-normal distribution; likewise, if X is...

Generalised Hyperbolic Secant or NEF-GHS distribution. A random variable follows a hyperbolic secant distribution if its probability density function...

function is the conditional expectation function, f s q ( x ) = E [ y x ] {\displaystyle f_{sq}(x)=\mathbb {E} \left[y_{x}\right]} ; For the logistic...

Vetterli, M. (February 2002). "Wavelet-based Texture Retrieval Using Generalised Gaussian Density and Kullback-Leibler Distance". IEEE Transactions on...

estimates β. Common choices for m include the logistic function. The data are often fitted as a generalised linear model where the predicted values μ are...

moment Generalised mean Image moment L-moment Method of moments (probability theory) Method of moments (statistics) Moment-generating function Moment...

regression Log-log plot Log-logistic distribution Logarithmic distribution Logarithmic mean Logistic distribution Logistic function Logistic regression Logit Logit...

dynamics of species competing for some common resource. They can be further generalised to the generalized Lotka–Volterra equation to include trophic interactions...

Riccati equation with constant coefficients equivalent to Verhulst—Pearl logistic growth. In 1969, Frank Bass published his paper on a new product growth...

functional forms, often versions of the generalised logistic growth such as the logistic, exponential or Gompertz functions. Though straightforward to fit with...

perceptrons and other models that were later found to be reinventions of the generalised linear models of statistics. Probabilistic reasoning was also employed...

Vargas, J. Mario (2006). "Obtaining Environmental Favourability Functions from Logistic Regression". Environmental and Ecological Statistics. 13 (2): 237–245...

{\displaystyle \mathbf {y} } given X {\displaystyle \mathbf {X} } to be a linear function of X {\displaystyle \mathbf {X} } and that the conditional variance of...

Climate change and the introduction of invasive species can affect the functioning of key species and thus have knock-on effects on the community processes...

points may be used to represent the levels of a categorical variable. A generalised biplot displays information on both continuous and categorical variables...

{\displaystyle \phi (x)} denote the standard normal probability density function ϕ ( x ) = 1 2 π e − x 2 2 {\displaystyle \phi (x)={\frac {1}{\sqrt {2\pi...

refers to neither randomness nor variability but instead is a mathematical function in which the domain is the set of possible outcomes in a sample space (e...

PMID 25353774. S2CID 22310350. da Silva, Sérgio Luiz E. F. (2021). "κ-generalised Gutenberg–Richter law and the self-similarity of earthquakes". Chaos...

application and generalisation of the logistic function (and equation). Applications include tests of chaos of the discrete logistic map, an endo-exo approach to...

all-important case of several serial components, MTBF calculation can be easily generalised into mtbf ( c 1 ; … ; c n ) = ( ∑ k = 1 n 1 mtbf ( c k ) ) − 1 , {\displaystyle...

scalable map (OS-Map) generalises the neighborhood function and the winner selection. The homogeneous Gaussian neighborhood function is replaced with the...