A first version of this theorem was proved by Friedrich Hartogs, and as such it is known also as Hartogs's lemma and Hartogs's principle: in earlier Soviet...

Tietze extension theorem Hartogs' extension theorem - a theorem in the theory of functions of several complex variables Isomorphism extension theorem - a...

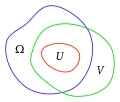
preparation theorem. A generalization of this theorem using the same method as Hartogs was proved in 2007. From Hartogs's extension theorem the domain...

geometry) Cramer's theorem (algebraic curves) (analytic geometry) Hartogs's theorem (complex analysis) Hartogs's extension theorem (several complex variables)...

in 1943. Hartogs' main work was in several complex variables where he is known for Hartogs's theorem, Hartogs's lemma (also known as Hartogs's principle...

than one variable are never discrete. This can be proved by Hartogs's extension theorem. Domains of holomorphy for single-valued functions consist of...

In set theory, the Schröder–Bernstein theorem states that, if there exist injective functions f : A → B and g : B → A between the sets A and B, then there...

the origin removed) is not an affine variety (compare this to Hartogs' extension theorem in complex analysis). See Spectrum of a ring § Non-affine examples...

_{\mathbb {R} ^{n}}|f|.} Hardy space Hardy space Hartogs 1.  Hartogs extension theorem 2.  Hartogs's theorem on separate holomorphicity harmonic A function...

S2CID 120514642, Zbl 0028.15301. In this work Severi gives his proof of the Hartogs' extension theorem. Severi, Francesco (1958), Lezioni sulle funzioni analitiche di...

has no poles of codimension one. This is an algebraic analog of Hartogs' extension theorem. There is also a relative version of this fact; see [2]. A morphism...

the Wayback Machine. In this paper Martinelli gives a proof of Hartogs' extension theorem by using the Bochner-Martinelli formula. Martinelli, Enzo (1984)...

Theory#Deformations of complex manifolds Enriques–Kodaira classification GAGA Hartogs' extension theorem Hermitian symmetric space Hodge decomposition Hopf manifold Imaginary...

proof Cantor's theorem Cantor–Bernstein–Schroeder theorem Cardinality Aleph number Aleph-null Aleph-one Beth number Cardinal number Hartogs number Cartesian...

February 17, 1964) was an Austrian mathematician, famous for the Tietze extension theorem on functions from topological spaces to the real numbers. He also...

the Wayback Machine. In this paper Martinelli gives a proof of Hartogs' extension theorem by using the Bochner-Martinelli formula. Martinelli, Enzo (1944–1945)...

Functional analysis The Hahn–Banach theorem in functional analysis, allowing the extension of linear functionals. The theorem that every Hilbert space has an...

cardinals between κ and its successor. (Without the axiom of choice, using Hartogs' theorem, it can be shown that for any cardinal number κ, there is a minimal...

holomorphic function of the remaining coordinate). The much deeper Hartogs' theorem proves that the continuity assumption is unnecessary: ⁠ f {\displaystyle...

(for fixed s) and s (for fixed z), and, thus, holomorphic on C × C by Hartog's theorem. Hence, the following decomposition γ ( s , z ) = z s Γ ( s ) γ ∗ (...

then there is a forcing extension in which 2 ℵ 0 = κ {\displaystyle 2^{\aleph _{0}}=\kappa } . However, per Kőnig's theorem, it is not consistent to...

one-to-one back into that set. That the set above is nonempty follows from Hartogs' theorem, which says that for any well-orderable cardinal, a larger such cardinal...

1090/s0002-9947-1961-0131756-3. MR 0131756. —— (1961). "A new proof and an extension of Hartog's theorem". Bull. Amer. Math. Soc. 67 (5): 507–509. doi:10.1090/s0002-9904-1961-10661-7...

theory E E(X) is the membership relation of the set X Easton's theorem Easton's theorem describes the possible behavior of the powerset function on regular...

_{n=1}^{\infty }\Omega _{n}} is also a domain of holomorphy (see Behnke-Stein theorem). If Ω 1 {\displaystyle \Omega _{1}} and Ω 2 {\displaystyle \Omega _{2}}...

squares Padé approximant Padé table — table of Padé approximants Hartogs–Rosenthal theorem — continuous functions can be approximated uniformly by rational...

even for infinite cardinals, and is known as Cantor–Bernstein–Schroeder theorem. Sets with cardinality of the continuum include the set of all real numbers...

be a polynomial. There is a counterpart of this theorem on the boundary, the Hartogs–Rosenthal theorem, which states that any continuous function ∂Ω can...

A n {\displaystyle \mathbb {A} ^{n}} when n ≥ 2: this is analogous to Hartogs's lemma in complex analysis, though easier to prove. That is, the inclusion...

The axiom schema of replacement is not necessary for the proofs of most theorems of ordinary mathematics. Indeed, Zermelo set theory (Z) already can interpret...