branches of mathematics, a topological space X is a T0 space or Kolmogorov space (named after Andrey Kolmogorov) if for every pair of distinct points of...

T3 if and only if it is both regular and T0. (A T0 or Kolmogorov space is a topological space in which any two distinct points are topologically distinguishable...

interpretation Kolmogorov microscales Kolmogorov's normability criterion Fréchet–Kolmogorov theorem Kolmogorov space Kolmogorov complexity Kolmogorov–Smirnov...

product space Kolmogorov space Lp-space Lens space Liouville space Locally finite space Loop space Lorentz space Mapping space Measure space Metric space Minkowski...

meaning.) A topological space is a T1 space if and only if it is both an R0 space and a Kolmogorov (or T0) space (i.e., a space in which distinct points...

distinguishable). A topological space is preregular if and only if its Kolmogorov quotient is Hausdorff. For a topological space X {\displaystyle X} , the following...

In statistics, the Kolmogorov–Smirnov test (also K–S test or KS test) is a nonparametric test of the equality of continuous (or discontinuous, see Section...

topological space. Moreover, for a uniformizable space X {\displaystyle X} the following are equivalent: X {\displaystyle X} is a Kolmogorov space X {\displaystyle...

In probability theory, Kolmogorov equations characterize continuous-time Markov processes. In particular, they describe how the probability of a continuous-time...

Remark. Completely regular spaces and Tychonoff spaces are related through the notion of Kolmogorov equivalence. A topological space is Tychonoff if and only...

information theory (a subfield of computer science and mathematics), the Kolmogorov complexity of an object, such as a piece of text, is the length of a shortest...

foundations of probability theory introduced by Russian mathematician Andrey Kolmogorov in 1933. These axioms remain central and have direct contributions to...

is always a Kolmogorov space (i.e., it satisfies the T0 separation axiom). However, a dcpo with the Scott topology is a Hausdorff space if and only if...

In probability theory, Kolmogorov's zero–one law, named in honor of Andrey Nikolaevich Kolmogorov, specifies that a certain type of event, namely a tail...

Taking Kolmogorov quotients, we see that all normal T1 spaces are Tychonoff. These are what we usually call normal Hausdorff spaces. A topological space is...

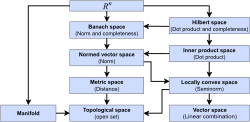
In mathematics, a Hilbert space is a real or complex inner product space that is also a complete metric space with respect to the metric induced by the...

In real analysis and approximation theory, the Kolmogorov–Arnold representation theorem (or superposition theorem) states that every multivariate continuous...

to that event. The Soviet mathematician Andrey Kolmogorov introduced the notion of a probability space and the axioms of probability in the 1930s. In...

The Kolmogorov–Arnold–Moser (KAM) theorem is a result in dynamical systems about the persistence of quasiperiodic motions under small perturbations. The...

of Markovian stochastic processes in probability theory, the Chapman–Kolmogorov equation (CKE) is an identity relating the joint probability distributions...

T0 or T00 may refer to: T0 space, a Kolmogorov space T0, a level on the tornado TORRO scale T−0, the end of a rocket's launch countdown and the beginning...

The following theorem is due to Kolmogorov: Kolmogorov's normability criterion: A Hausdorff topological vector space is normable if and only if there...

In fluid dynamics, Kolmogorov microscales are the smallest scales in turbulent flow. At the Kolmogorov scale, viscosity dominates and the turbulence kinetic...

mathematics, the Kolmogorov extension theorem (also known as Kolmogorov existence theorem, the Kolmogorov consistency theorem or the Daniell-Kolmogorov theorem)...

introduced by John von Neumann and Andrey Kolmogorov in 1935. Suppose X {\displaystyle X} is a topological vector space (TVS) over a topological field K . {\displaystyle...

{C}}(a,b)} is called the uniform norm or supremum norm ('sup norm'). Kolmogorov, A. N., & Fomin, S. V. (1967). Elements of the theory of functions and...

 262. hdl:2027/mdp.49015000696204. Cf. definition 39.7 and lemma 39.8. Kolmogorov, A. N.; Fomin, S. V. (1957) [1954]. Elements of the theory of functions...

is not, in general, a T1 space. However, Spec ⁡ ( R ) {\displaystyle \operatorname {Spec} (R)} is always a Kolmogorov space (satisfies the T0 axiom);...

Anatoliy Skorokhod and Andrei Kolmogorov, for a continuous-time stochastic process with any metric space as its state space. For the construction of such...

In functional analysis, the Fréchet–Kolmogorov theorem (the names of Riesz or Weil are sometimes added as well) gives a necessary and sufficient condition...