The Lenstra elliptic-curve factorization or the elliptic-curve factorization method (ECM) is a fast, sub-exponential running time, algorithm for integer...

integer factorization algorithms that have applications in cryptography, such as Lenstra elliptic-curve factorization. The use of elliptic curves in cryptography...

called prime factorization; the result is always unique up to the order of the factors by the prime factorization theorem. To factorize a small integer...

mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point O. An elliptic curve is defined over...

Discovering the elliptic curve factorization method (in 1987); Computing all solutions to the inverse Fermat equation (in 1992); The Cohen-Lenstra heuristics...

Wikiversity has learning resources about Quadratic Sieve Lenstra elliptic curve factorization primality test Carl Pomerance, Analysis and Comparison of...

Morain [de], in 1993. The concept of using elliptic curves in factorization had been developed by H. W. Lenstra in 1985, and the implications for its use...

circuits. In 2012, the factorization of 15 {\displaystyle 15} was performed with solid-state qubits. Later, in 2012, the factorization of 21 {\displaystyle...

Elliptic-curve Diffie–Hellman (ECDH) is a key agreement protocol that allows two parties, each having an elliptic-curve public–private key pair, to establish...

integer factorization algorithms, such as Pollard's rho algorithm, Shor's algorithm, Dixon's factorization method and the Lenstra elliptic curve factorization...

Elliptic curve scalar multiplication is the operation of successively adding a point along an elliptic curve to itself repeatedly. It is used in elliptic...

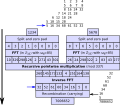
approximations of π, as well as practical applications such as Lenstra elliptic curve factorization via Kronecker substitution, which reduces polynomial multiplication...

primality test Pollard's p − 1 algorithm Pollard's rho algorithm Lenstra elliptic curve factorization Quadratic sieve Special number field sieve General number...

General number field sieve Lenstra elliptic curve factorization Pollard's p − 1 algorithm Pollard's rho algorithm prime factorization algorithm Quadratic sieve...

Digital Signature Algorithm) and cyclic subgroups of elliptic curves over finite fields (see Elliptic curve cryptography). While there is no publicly known...

calculator can factorize any positive integer up to 20 digits. Fast Online primality test with factorization makes use of the Elliptic Curve Method (up to...

integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not. Factorization is thought...

3, 2, 1, 2, 3, 1, 2, ... (sequence A046072 in the OEIS) Lenstra elliptic curve factorization Weisstein, Eric W. "Modulo Multiplication Group". MathWorld...

887 (≈1.81×1072) – The largest known prime factor found by Lenstra elliptic-curve factorization (LECF) as of 2010[update]. Mathematics: There are 282,870...

Goro Shimura and Yutaka Taniyama suspected a link might exist between elliptic curves and modular forms, two completely different areas of mathematics. Known...

integer factorization: a proposal". cr.yp.to. Arjen K. Lenstra; Adi Shamir; Jim Tomlinson; Eran Tromer (2002). "Analysis of Bernstein's Factorization Circuit"...

network. Trafford. p. 167. ISBN 978-1466985742. Lenstra, Arjen; et al. (Group) (2000). "Factorization of a 512-bit RSA Modulus" (PDF). Eurocrypt. Miller...

The Lenstra–Lenstra–Lovász (LLL) lattice basis reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik...

Pollard's p − 1 algorithm is a number theoretic integer factorization algorithm, invented by John Pollard in 1974. It is a special-purpose algorithm,...

"Factorization of RSA-250". Cado-nfs-discuss. Archived from the original on 2020-02-28. Retrieved 2020-07-12. "Certicom Announces Elliptic Curve Cryptography...

context-sensitive help BASIC List of BASIC dialects by platform Lenstra elliptic curve factorization complex numbers Prime number Jørgen Pedersen Gram Logarithmic...

it is a proper factorization of N. Each odd number has such a representation. Indeed, if N = c d {\displaystyle N=cd} is a factorization of N, then N =...

Kleinjung, Arjen K. Lenstra and Peter L. Montgomery announced that they had carried out a discrete logarithm computation on an elliptic curve (known as secp112r1)...

against modulus factorisation using newer algorithms such as Lenstra elliptic curve factorization and Number Field Sieve algorithm. Given the additional cost...

family of algorithms adapted to finite fields and to some families of elliptic curves. The algorithm collects relations among the discrete logarithms of...