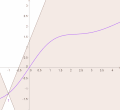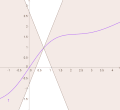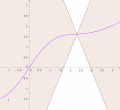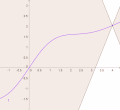
mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively...

Cauchy–Lipschitz theorem Lipschitz domain Lipschitz quaternion Lipschitz continuity Uniform, Hölder and Lipschitz continuity Lipschitz distance Lipschitz-continuous...

= 1 {\displaystyle \alpha =1} is referred to as Lipschitz continuity. That is, a function is Lipschitz continuous if there is a constant K such that the...

the same modulus of continuity are exactly equicontinuous families. For instance, the modulus ω(t) := kt describes the k-Lipschitz functions, the moduli...

absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows...

: R n → R m {\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}} is Lipschitz continuous (with the appropriate normed spaces as needed) in the neighbourhood...

describe a function that satisfies the Lipschitz condition, a strong form of continuity, named after Rudolf Lipschitz. The surname may refer to: Daniel Lipšic...

h} is an example of a function that is differentiable but not locally Lipschitz continuous. The exponential function e x {\displaystyle e^{x}} is analytic...

However, any Lipschitz map between metric spaces is uniformly continuous, in particular any isometry (distance-preserving map). Although continuity can be defined...

{\displaystyle L} is uniformly continuous, and even Lipschitz continuous. Conversely, it follows from the continuity at the zero vector that there exists a ε >...

Rudolf Lipschitz. Let f be a function on [0,2π], let t be some point and let δ be a positive number. We define the local modulus of continuity at the...

a violation of the principle of Lipschitz continuity (the force that appears in Newton's second law is not a Lipschitz continuous function of the particle's...

the endpoints of the curves and both of which obey a Lipschitz continuity condition with Lipschitz constant less than one. Tao also formulated several...

In mathematics, the Dini–Lipschitz criterion is a sufficient condition for the Fourier series of a periodic function to converge uniformly at all real...

condition and local martingale property. Uniqueness follows from the Lipschitz continuity of σ , b {\displaystyle \sigma \!,\!b} . In fact, L a ; b + ∂ ∂ s...

mathematical analysis, Dini continuity is a refinement of continuity. Every Dini continuous function is continuous. Every Lipschitz continuous function is...

Itô process, provided μ , σ {\displaystyle \mu ,\sigma } satisfy Lipschitz continuity and linear growth conditions with respect to x {\displaystyle x}...

local Lipschitz constant for the gradient ∇ f {\displaystyle \nabla f\,} near the point x {\displaystyle \mathbf {x} } (see Lipschitz continuity). If the...

Rosen (EPR paradox); Moshe Carmeli (Gauge theory). Rudolf Lipschitz (Lipschitz continuity); Paul Cohen (Continuum hypothesis, Axiom of choice); Laurent...

assumes more and concludes more. It requires Lipschitz continuity, while the Peano theorem requires only continuity; but it proves both existence and uniqueness...

of a function Uniform continuity Modulus of continuity Lipschitz continuity Semi-continuity Equicontinuous Absolute continuity Hölder condition – condition...

topology and algebraic geometry. The Hirzebruch–Riemann–Roch theorem, Lipschitz continuity, the Petri net, the Schönhage–Strassen algorithm, Faltings's theorem...

well as uniform, Lipschitz, and Hölder continuity, can be defined in the setting of metric spaces. Other notions, such as continuity, compactness, and...

worked on the Dirichlet principle Rudolf Lipschitz (1832–1903), mathematician, named the Lipschitz continuity condition Alfred Clebsch (1833–1872), mathematician...

is constant (see proof below). If α = 1, then the function satisfies a Lipschitz condition. For any α > 0, the condition implies the function is uniformly...

[ 0 , 1 ] {\textstyle t\in [0,1]} and use the L {\textstyle L} -Lipschitz continuity to show that f ( y ) − f ( x ) = g ( 1 ) − g ( 0 ) = ∫ 0 1 g ′ (...

analysis) Kachurovskii's theorem (convex analysis) Kirszbraun theorem (Lipschitz continuity) M. Riesz extension theorem (functional analysis) Milman–Pettis theorem...

For linear operators between normed vector spaces, Lipschitz continuity is equivalent to continuity—an operator satisfying either of these conditions is...

closure axioms Unicoherent Solenoid (mathematics) Uniform continuity Lipschitz continuity Uniform isomorphism Uniform property Uniformly connected space...

Brownian motion and b : Rn → Rn and σ : Rn → Rn×m satisfy the usual Lipschitz continuity condition | b ( x ) − b ( y ) | + | σ ( x ) − σ ( y ) | ≤ C | x −...