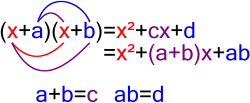In mathematics, a matrix factorization of a polynomial is a technique for factoring irreducible polynomials with matrices. David Eisenbud proved that...

integer factorization of 15, and (x − 2)(x + 2) is a polynomial factorization of x2 − 4. Factorization is not usually considered meaningful within number...

Polynomial Matrix Spectral Factorization or Matrix Fejer–Riesz Theorem is a tool used to study the matrix decomposition of polynomial matrices. Polynomial...

mathematics and computer algebra the factorization of a polynomial consists of decomposing it into a product of irreducible factors. This decomposition...

mathematics and computer algebra, factorization of polynomials or polynomial factorization expresses a polynomial with coefficients in a given field or in the integers...

test irreducibility and to compute the factorization into irreducible polynomials (see Factorization of polynomials). These algorithms are not practicable...

square-free factorization of the polynomial, which provides polynomials whose roots are the roots of a given multiplicity of the original polynomial. The greatest...

linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as...

eigendecomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors...

semidefinite matrix A as BTB = A, as in the Cholesky factorization, even if BB ≠ A. This distinct meaning is discussed in Positive definite matrix § Decomposition...

Non-negative matrix factorization (NMF or NNMF), also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra...

minimal polynomial μA of an n × n matrix A over a field F is the monic polynomial P over F of least degree such that P(A) = 0. Any other polynomial Q with...

methods of solution are computationally much more efficient. Determinants are used for defining the characteristic polynomial of a square matrix, whose...

into a more easily accessible form. They are generally referred to as matrix decomposition or matrix factorization techniques. The interest of all these...

the polynomial and its derivative. The square-free factorization of a polynomial p is a factorization p = p 1 p 2 2 ⋯ p k k {\displaystyle p=p_{1}p_{2}^{2}\cdots...

means that the Vandermonde matrix is the design matrix of polynomial regression. In numerical analysis, solving the equation V a = y {\displaystyle Va=y}...

situation is better than for integer factorization, as there are factorization algorithms that have a polynomial complexity. They are implemented in most...

constant α > 0 {\displaystyle \alpha >0} is a polynomial time algorithm. The following table summarizes some classes of commonly encountered time complexities...

an invertible matrix is a square matrix that has an inverse. In other words, if some other matrix is multiplied by the invertible matrix, the result can...

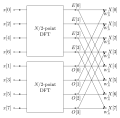
interpreting the FFT as a recursive factorization of the polynomial z n − 1 {\displaystyle z^{n}-1} , here into real-coefficient polynomials of the form z m −...

Furthermore, a similar factorization holds for any n × n rotation matrix. If the dimension, n, is odd, there will be a "dangling" eigenvalue of 1; and for any...

they evaluate to zero. Factorization consists of rewriting a polynomial as a product of several factors. For example, the polynomial x 2 − 3 x − 10 {\displaystyle...

n} matrix A {\displaystyle A} , called the transformation matrix of T {\displaystyle T} , such that: T ( x ) = A x {\displaystyle T(\mathbf {x} )=A\mathbf...

Subsequent reduction of Hessenberg matrix to a triangular matrix can be achieved through iterative procedures, such as shifted QR-factorization. In eigenvalue...

Its factorization was announced on April 1, 1991, by Arjen K. Lenstra. Reportedly, the factorization took a few days using the multiple-polynomial quadratic...

multiplication operator by a trigonometric polynomial, compressed to a finite-dimensional space, can be represented by such a matrix. Similarly, one can represent...

In mathematics and computer science, polynomial evaluation refers to computation of the value of a polynomial when its indeterminates are substituted for...

Cholesky factorization (pronounced /ʃəˈlɛski/ shə-LES-kee) is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular...

yields a zero remainder, indicating that r1(x) is the greatest common divisor polynomial of a(x) and b(x), consistent with their factorization. Many of the...

multivariate polynomial is the 0-polynomial, the polynomial that ignores all its variables and always returns zero. The lemma states that evaluating a nonzero...