orientation of a real vector bundle is a generalization of an orientation of a vector space; thus, given a real vector bundle π: E →B, an orientation...
4 KB (657 words) - 00:49, 22 February 2022
Orientability (redirect from Orientation of a manifold)
take two copies of M {\displaystyle M} , each of which corresponds to a different orientation. A real vector bundle, which a priori has a GL(n) structure...
25 KB (3,553 words) - 03:19, 5 April 2025
The orientation of a real vector space or simply orientation of a vector space is the arbitrary choice of which ordered bases are "positively" oriented...
15 KB (1,988 words) - 07:04, 7 April 2025
bundle. A sphere bundle that is a product space is orientable, as is any sphere bundle over a simply connected space. If E be a real vector bundle on a space...
3 KB (377 words) - 16:47, 28 June 2022
Euler class (category Vector bundles)
class is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is. In...
11 KB (2,003 words) - 20:31, 8 May 2025
Chern class (category Pages that use a deprecated format of the math tags)
characteristic classes associated with complex vector bundles. They have since become fundamental concepts in many branches of mathematics and physics, such as string...
42 KB (7,508 words) - 13:07, 21 April 2025
Thom space (section Construction of the Thom space)
Thom and Lev Pontryagin) of algebraic topology and differential topology is a topological space associated to a vector bundle, over any paracompact space...
13 KB (1,983 words) - 18:16, 2 December 2024
made, since the density bundle is the tensor product of the orientation bundle of M and the n-th exterior product bundle of T∗M (see pseudotensor). In...
9 KB (1,562 words) - 12:22, 28 July 2024
In mathematics, a symplectic vector space is a vector space V {\displaystyle V} over a field F {\displaystyle F} (for example the real numbers R {\displaystyle...
15 KB (2,275 words) - 11:50, 14 August 2024
of the ambient space minus the dimension of the submanifold. Connected sum Connection Cotangent bundle – the vector bundle of cotangent spaces on a manifold...
7 KB (869 words) - 08:54, 6 December 2024
In mathematics, a vector bundle is said to be flat if it is endowed with a linear connection with vanishing curvature, i.e. a flat connection. Let π :...
3 KB (417 words) - 22:26, 21 September 2021
physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has...
61 KB (9,116 words) - 12:01, 7 May 2025
group of the frame bundle to G {\displaystyle G} . The following examples are defined for real vector bundles, particularly the tangent bundle of a smooth...
20 KB (2,576 words) - 06:58, 26 June 2023
algebra. A vector bundle is a family of vector spaces parametrized continuously by a topological space X. More precisely, a vector bundle over X is a topological...
87 KB (11,491 words) - 12:05, 7 May 2025
Tensor (redirect from Tensor on a vector space)
mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors...
69 KB (9,357 words) - 20:21, 20 April 2025
Differential form (redirect from Integration of a differential form)
{R} } defines a linear functional on each tangent space of M, and therefore it factors through the trivial bundle M × R. The vector bundle morphism ⋀ k...
67 KB (10,058 words) - 03:02, 23 March 2025
Differentiable manifold (redirect from Sheaf of smooth functions)
products of the tangent bundle and the cotangent bundle. Each element of the bundle is a tensor field, which can act as a multilinear operator on vector fields...
67 KB (9,497 words) - 20:48, 13 December 2024
Gauge theory (mathematics) (section Vector bundles)
physics, gauge theory is the general study of connections on vector bundles, principal bundles, and fibre bundles. Gauge theory in mathematics should not...
72 KB (11,468 words) - 19:43, 14 May 2025
Covariant derivative (section Vector fields)
straightforwardly to a notion of differentiation associated to a connection on a vector bundle, also known as a Koszul connection. Historically, at the turn of the 20th...
37 KB (6,453 words) - 09:24, 15 May 2025
Metric connection (redirect from Compatibility of the metric)
mathematics, a metric connection is a connection in a vector bundle E equipped with a bundle metric; that is, a metric for which the inner product of any two...
18 KB (3,283 words) - 23:21, 7 January 2024
Spinor (redirect from Spin vector)
roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the...
72 KB (9,924 words) - 14:30, 4 May 2025
Normal (geometry) (redirect from Normal orientation)
point. A normal vector is a vector perpendicular to a given object at a particular point. A normal vector of length one is called a unit normal vector or...
17 KB (2,664 words) - 16:29, 1 April 2025
Exterior algebra (redirect from Extended vector algebra)
Grassmann algebra of a vector space V {\displaystyle V} is an associative algebra that contains V , {\displaystyle V,} which has a product, called exterior...
77 KB (12,118 words) - 20:04, 2 May 2025
Basis (linear algebra) (redirect from Basis of a vector space)
mathematics, a set B of elements of a vector space V is called a basis (pl.: bases) if every element of V can be written in a unique way as a finite linear...
34 KB (4,751 words) - 04:52, 13 April 2025
Curl (mathematics) (redirect from Rotation of a vector field)
In vector calculus, the curl, also known as rotor, is a vector operator that describes the infinitesimal circulation of a vector field in three-dimensional...
34 KB (5,050 words) - 04:31, 3 May 2025
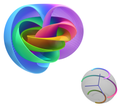
Hopf fibration (redirect from Hopf bundle)
fibration (also known as the Hopf bundle or Hopf map) describes a 3-sphere (a hypersphere in four-dimensional space) in terms of circles and an ordinary sphere...
36 KB (4,813 words) - 13:13, 9 April 2025
Serre duality (category Topological methods of algebraic geometry)
varieties, proved by Jean-Pierre Serre. The basic version applies to vector bundles on a smooth projective variety, but Alexander Grothendieck found wide...
18 KB (3,295 words) - 02:08, 27 December 2024
Volume form (section Orientation)
a principal G L + ( n ) {\displaystyle \mathrm {GL} ^{+}(n)} sub-bundle of the linear frame bundle of M , {\displaystyle M,} and so the orientation associated...
14 KB (2,341 words) - 15:01, 22 February 2025
Orthogonal group (redirect from Invariant theory of the orthogonal group)
π0(KO) is a vector bundle over S0, which consists of two points. Thus over each point, the bundle is trivial, and the non-triviality of the bundle is the...
56 KB (7,881 words) - 20:44, 2 May 2025
Hodge star operator (redirect from Dual of a tensor)
operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric...
40 KB (6,501 words) - 19:54, 12 May 2025