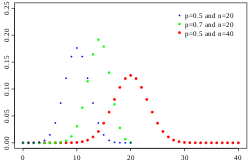
In probability theory, the law of rare events or Poisson limit theorem states that the Poisson distribution may be used as an approximation to the binomial...

distance. By setting pi = λn/n, we see that this generalizes the usual Poisson limit theorem. When λ n {\displaystyle \lambda _{n}} is large a better bound is...

In probability theory, the central limit theorem (CLT) states that, under appropriate conditions, the distribution of a normalized version of the sample...

distribution converges to what is known as the Poisson distribution by the Poisson limit theorem. In several of the above examples — such as the number of mutations...

10. Concerning the accuracy of Poisson approximation, see Novak, ch. 4, and references therein. Poisson limit theorem: As n approaches ∞ and p approaches...

In probability theory, the central limit theorem states that, under certain circumstances, the probability distribution of the scaled mean of a random...

In probability theory, the de Moivre–Laplace theorem, which is a special case of the central limit theorem, states that the normal distribution may be...

Baron Siméon Denis Poisson (/pwɑːˈsɒ̃/, US also /ˈpwɑːsɒn/; French: [si.me.ɔ̃ də.ni pwa.sɔ̃]; 21 June 1781 – 25 April 1840) was a French mathematician...

representation theorem (probability theory) Maxwell's theorem (probability theory) Optional stopping theorem (probability theory) Poisson limit theorem (probability)...

process Poisson binomial distribution Poisson distribution Poisson hidden Markov model Poisson limit theorem Poisson process Poisson regression Poisson random...

statistics and related fields, a Poisson point process (also known as: Poisson random measure, Poisson random point field and Poisson point field) is a type of...

In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values...

a field in mathematics, a Poisson manifold is a smooth manifold endowed with a Poisson structure. The notion of Poisson manifold generalises that of...

(T\cdot x(nT))} in Poisson's formula (Eq.1), and, on the right, the actual formula for Fourier expansion coefficients. The sampling theorem is usually formulated...

In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's...

properties analogous to the strong law of large numbers and central limit theorem. The renewal function m ( t ) {\displaystyle m(t)} (expected number...

typically, quantum commutators (equivalently, Moyal brackets) reduce to Poisson brackets, in a group contraction. In quantum mechanics, due to Heisenberg's...

sampling Poisson scatter theorem Poisson random measure Poisson-type random measure Poisson regression Fixed-effect Poisson model Poisson limit theorem Poisson...

_{t}\}_{t\geq 0}} with this distribution. Cramér's theorem Indecomposable distribution Compound Poisson distribution Lukacs, E. (1970) Characteristic Functions...

In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem relating the flux of a vector field through...

(and the theorem) does not say anything about the limit of the difference of the two functions as x increases without bound. Instead, the theorem states...

{\displaystyle \mu /p} , with the distribution becoming identical to Poisson in the limit p → 1 {\displaystyle p\to 1} for a given mean μ {\displaystyle \mu...

discipline within the mathematical theory of probability, the arrival theorem (also referred to as the random observer property, ROP or job observer...

statistics, Poisson regression is a generalized linear model form of regression analysis used to model count data and contingency tables. Poisson regression...

Gaussian distributions, the purely discrete scaled Poisson distribution, and the class of compound Poisson–gamma distributions which have positive mass at...

found the limiting case, which is effectively recasting the Poisson distribution as a limit of the binomial distribution. In 1910, Ernest Rutherford and...

In probability theory and statistics, the Poisson binomial distribution is the discrete probability distribution of a sum of independent Bernoulli trials...

finding a (quantum) algebra whose classical limit is a given (classical) algebra such as a Lie algebra or a Poisson algebra. Intuitively, a deformation of...

Phase space Symplectic manifold Liouville's theorem (Hamiltonian) Poisson bracket Poisson algebra Poisson manifold Antibracket algebra Hamiltonian constraint...

theorem may also be proved based on complex integration of a doubly periodic function related to Weierstrass elliptic functions. Applying the Poisson...