Schoof's algorithm is an efficient algorithm to count points on elliptic curves over finite fields. The algorithm has applications in elliptic curve cryptography...

trace the developments up to Schoof's definitive work on the subject, while also listing the improvements to Schoof's algorithm made by Elkies (1990) and...

application is in elliptic curve cryptography. The algorithm is an extension of Schoof's algorithm by Noam Elkies and A. O. L. Atkin to significantly...

central role in the study of counting points on elliptic curves in Schoof's algorithm. The set of division polynomials is a sequence of polynomials in Z...

football player Schoof cabinet Schoofs 17958 Schoof, a main-belt asteroid Schoof–Elkies–Atkin algorithm, extension of Schoof's algorithm by Noam Elkies...

E using Schoof's algorithm, which is the preferred algorithm for the Goldwasser–Kilian algorithm. However, the original algorithm by Schoof is not efficient...

Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor...

curve and use a general point-counting algorithm, for example, Schoof's algorithm or the Schoof–Elkies–Atkin algorithm, Select a random curve from a family...

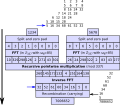
multiplication algorithm is an algorithm (or method) to multiply two numbers. Depending on the size of the numbers, different algorithms are more efficient...

Z/36Z. The number of points on a specific curve can be computed with Schoof's algorithm. Studying the curve over the field extensions of Fq is facilitated...

proved by André Weil in the case of curves. Sato–Tate conjecture Schoof's algorithm Weil's bound Artin, Emil (1924), "Quadratische Körper im Gebiete der...

stages. He also wrote a book on Catalan's conjecture. Schoof's algorithm Schoof–Elkies–Atkin algorithm Homepage Counting points of elliptic curves over finite...

Harvard's history. He and A. O. L. Atkin extended Schoof's algorithm to create the Schoof–Elkies–Atkin algorithm. Elkies also studies the connections between...

Chicago. Atkin, along with Noam Elkies, extended Schoof's algorithm to create the Schoof–Elkies–Atkin algorithm. Together with Daniel J. Bernstein, he developed...

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers...

The Karatsuba algorithm is a fast multiplication algorithm for integers. It was discovered by Anatoly Karatsuba in 1960 and published in 1962. It is a...

Pollard's rho algorithm is an algorithm for integer factorization. It was invented by John Pollard in 1975. It uses only a small amount of space, and...

Pollard's p − 1 algorithm is a number theoretic integer factorization algorithm, invented by John Pollard in 1974. It is a special-purpose algorithm, meaning...

and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common...

theory, Williams's p + 1 algorithm is an integer factorization algorithm, one of the family of algebraic-group factorisation algorithms. It was invented by...

The binary GCD algorithm, also known as Stein's algorithm or the binary Euclidean algorithm, is an algorithm that computes the greatest common divisor...

Pollard's rho algorithm for logarithms is an algorithm introduced by John Pollard in 1978 to solve the discrete logarithm problem, analogous to Pollard's...

A division algorithm is an algorithm which, given two integers N and D (respectively the numerator and the denominator), computes their quotient and/or...

The Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen...

a_{1}x_{1}+a_{2}x_{2}+\cdots +a_{n}x_{n}=0.\,} An integer relation algorithm is an algorithm for finding integer relations. Specifically, given a set of real...

efficient non-quantum integer factorization algorithm is known. However, it has not been proven that such an algorithm does not exist. The presumed difficulty...

In computational number theory, the index calculus algorithm is a probabilistic algorithm for computing discrete logarithms. Dedicated to the discrete...

kangaroo algorithm (also Pollard's lambda algorithm, see Naming below) is an algorithm for solving the discrete logarithm problem. The algorithm was introduced...

Lenstra–Lenstra–Lovász (LLL) lattice basis reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and...

Lehmer's GCD algorithm, named after Derrick Henry Lehmer, is a fast GCD algorithm, an improvement on the simpler but slower Euclidean algorithm. It is mainly...