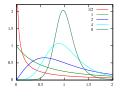
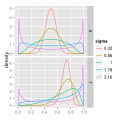
and statistics, the log-logistic distribution (known as the Fisk distribution in economics) is a continuous probability distribution for a non-negative...

statistics, the logistic distribution is a continuous probability distribution. Its cumulative distribution function is the logistic function, which appears...

The shifted log-logistic distribution is a probability distribution also known as the generalized log-logistic or the three-parameter log-logistic distribution...

other families of distributions that have also been called generalized logistic distributions, see the shifted log-logistic distribution, which is a generalization...

cumulative distribution function of the shifted Gompertz distribution, and the hyperbolastic function of type I. In statistics, where the logistic function...

the Wald distribution The Lévy distribution The log-Cauchy distribution The log-Laplace distribution The log-logistic distribution The log-metalog distribution...

distributed, then Y = logit(X)= log (X/(1-X)) is normally distributed. It is also known as the logistic normal distribution, which often refers to a multinomial...

In statistics, multinomial logistic regression is a classification method that generalizes logistic regression to multiclass problems, i.e. with more than...

Gompertz distribution Shifted log-logistic distribution Shifting baseline Shrinkage (statistics) Shrinkage estimator Sichel distribution Siegel–Tukey test...

scaled and shifted square of a standard normal variable, it is distributed as a scaled and shifted chi-squared variable. The distribution of the variable...

{\text{Beta}}(\alpha ,\beta )} , then Y = log ⁡ X 1 − X {\displaystyle Y=\log {\frac {X}{1-X}}} has a generalized logistic distribution, with density σ ( y ) α σ (...

follows a logistic distribution with location log(λ) and scale 1.0. The Lomax distribution arises as a mixture of exponential distributions where the...

statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional...

The logistic map is a discrete dynamical system defined by the quadratic difference equation: Equivalently it is a recurrence relation and a polynomial...

Singh–Maddala distribution. β ′ ( 1 , 1 , γ , σ ) = LL ( γ , σ ) {\displaystyle \beta '(1,1,\gamma ,\sigma )={\textrm {LL}}(\gamma ,\sigma )} the log logistic distribution...

probability distribution of K possible outcomes. It is a generalization of the logistic function to multiple dimensions, and is used in multinomial logistic regression...

f(w) = wew, and of the logistic function, respectively. From the perspective of group theory, the identity log(cd) = log(c) + log(d) expresses a group isomorphism...

the log-logistic distribution (i.e. the log values of the data follow a logistic distribution), the Gumbel distribution, the exponential distribution, the...

{\displaystyle I[f]} for the logistic loss function can be directly found from equation (1) as f Logistic ∗ = log ⁡ ( η 1 − η ) = log ⁡ ( p ( 1 ∣ x ) 1 − p (...

this case the distribution is a normal distribution, otherwise the distributions are shifted and possibly reversed log-normal distributions. Parameters...

Laplace distributions are extensions of the Laplace distribution and the asymmetric Laplace distribution to multiple variables. The marginal distributions of...

argument set to zero is the multivariable generalization of the logistic function. Both LogSumExp and softmax are used in machine learning. Exponential linear...

power distribution Fréchet distribution Gamma distribution Generalized extreme value distribution Log-logistic distribution Log-t distribution Inverse-gamma...

logarithm log ⁡ ( X i ) {\displaystyle \log(X_{i})} : X i log ⁡ ( X i ) {\displaystyle X_{i}\log(X_{i})} This term is included in the logistic regression...

Kumaraswamy distribution Log-logistic distribution (Fisk distribution): Let β be the shape parameter. The variance and mean of this distribution are only...

a binomial distribution and implicitly assumes an approximately normal distribution. k = ⌈ log 2 ⁡ n ⌉ + 1 , {\displaystyle k=\lceil \log _{2}n\rceil...

only positive values approaches a normal distribution, the product itself approaches a log-normal distribution. Many physical quantities (especially mass...

{\displaystyle n} ) the model can support is 4, because log ⁡ 1000 log ⁡ 5 ≈ 4.29 {\displaystyle {\frac {\log 1000}{\log 5}}\approx 4.29} . Although the parameters...

+ e − x exp ⁡ ( − θ log ⁡ ( 1 + e − x ) + log ⁡ ( θ ) ) {\displaystyle {\frac {e^{-x}}{1+e^{-x}}}\exp(-\theta \log(1+e^{-x})+\log(\theta ))} which is...

a chi-squared distribution ( p − n + 1 2 − m ) log ⁡ Λ ( p , m , n ) ∼ χ n p 2 . {\displaystyle \left({\frac {p-n+1}{2}}-m\right)\log \Lambda (p,m,n)\sim...