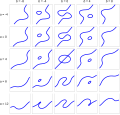
geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends...

mathematical field of algebraic geometry, a singular point of an algebraic variety V is a point P that is 'special' (so, singular), in the geometric sense...

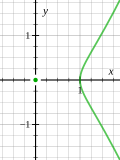
as of endpoint. This point is the only singular point of the curve. There are also two arcs having this singular point as one endpoint and having a second...

at which a given mathematical object is not defined or not "well-behaved", for example infinite or not differentiable Singular point of a curve, where the...

typical example is given in the figure. A cusp is thus a type of singular point of a curve. For a plane curve defined by an analytic, parametric equation...

an infinite cardinal number that is not a regular cardinal Singular point of a curve, in geometry Singularity (disambiguation) Singulair, Merck trademark...

point, Regular singular point Saddle point Semistable point Separable point Simple point Singular point of a curve Singular point of an algebraic variety...

A cubic curve may have a singular point, in which case it has a parametrization in terms of a projective line. Otherwise a non-singular cubic curve is...

algebraic geometry, a tacnode (also called a point of osculation or double cusp) is a kind of singular point of a curve. It is defined as a point where two (or...

such singular points must be counted with multiplicity (2 for a double point, 3 for a cusp), in accounting for intersections of curves. It was then a short...

connected components by a function of the degrees of the polynomials that define the variety. Singular point of a curve Singularity theory Milnor, John (1963)...

Position (geometry) Point at infinity Point cloud Point process Point set registration Pointwise Singular point of a curve Whitehead point-free geometry Ohmer...

geometry, an inflection point, point of inflection, flex, or inflection (rarely inflexion) is a point on a smooth plane curve at which the curvature changes...

also refer to: Cusp (singularity), a singular point of a curve Cusp catastrophe, a branch of bifurcation theory in the study of dynamical systems Cusp...

mathematics, a crunode (archaic; from Latin crux "cross" + node) or node of an algebraic curve is a type of singular point at which the curve intersects...

critical point Singular point of an algebraic variety, a type of singular point of a curve node, the points where a great circle crosses a plane of reference...

elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point O. An elliptic curve is defined over a field K...

non-singular, elliptic curves. Those of degree 4 are called quartic plane curves. Numerous examples of plane curves are shown in Gallery of curves and...

and a cylinder: one part Intersection of a sphere and a cylinder: two parts Intersection of a sphere and a cylinder: curve with one singular point Intersection...

defines a quadratic extension of C(x), and it is that function field that is meant. The singular point at infinity can be removed (since this is a curve) by...

In mathematics, a singularity is a point at which a given mathematical object is not defined, or a point where the mathematical object ceases to be well-behaved...

thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's Elements: "The [curved] line is...

geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve...

simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it...

used to mean a solution at which there is a failure of uniqueness to the initial value problem at every point on the curve. A singular solution in this...

local maximum at the singularity. Singular point of a curve Crunode Cusp Tacnode Hazewinkel, M. (2001) [1994], "Acnode", Encyclopedia of Mathematics, EMS...

property of having non-trivial endomorphisms rather than referring to a singular curve. The modular function j(τ) is algebraic on imaginary quadratic numbers...

conditions. The set of the points that satisfy some property is often called the locus of a point satisfying this property. The use of the singular in this formulation...

arithmetic genus of the curve. Noether's method takes a plane curve and repeatedly applies quadratic transformations (determined by a singular point and two points...

example, an elliptic curve (a non-singular genus 1 curve with 1 marked point) is stable. Over the complex numbers, a connected curve is stable if and only...