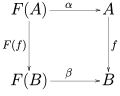
especially in category theory, a subobject classifier is a special object Ω of a category such that, intuitively, the subobjects of any object X in the category...

e.g.: Hierarchical classifier Linear classifier Deductive classifier Subobject classifier, in category theory An air classifier or similar machine for...

category will be monomorphisms. A subobject of a terminal object is called a subterminal object. Subobject classifier Subquotient Mac Lane, p. 126 Mac...

The category has a subobject classifier. The category is Cartesian closed. In some applications, the role of the subobject classifier is pivotal, whereas...

subobject classifier. This subobject classifier functions like the set of all possible truth values. In the topos of sets, the subobject classifier is...

the subobject classifier. In particular, in a topos every formula of higher-order logic may be assigned a truth value in the subobject classifier. Even...

domain of a double integral. In topos theory, the (codomain of the) subobject classifier of an elementary topos. In combinatory logic, the looping combinator...

generalization of a topos. A topos has a subobject classifier classifying all subobjects, but in a quasitopos, only strong subobjects are classified. Quasitoposes...

Heyting algebra of subobjects of the terminal object 1 ordered by inclusion, equivalently the morphisms from 1 to the subobject classifier Ω. The open sets...

Set in some well-defined way. Every two-element set serves as a subobject classifier in Set. The power object of a set A is given by its power set, and...

variable (statistics) Statistical classification Zero-one loss function Subobject classifier, a related concept from topos theory. The Greek letter χ appears...

closed (and moreover cartesian closed) and has an object Ω, called a subobject classifier. Although the term "power object" is sometimes used synonymously...

category (it can be written down explicitly, and is related to the subobject classifier). This is enough to show that right derived functors of any left...

space-time based on category-theoretic notions of a topos and its subobject classifier (which has a Heyting algebra structure, but not necessarily a Boolean...

right-adjoint G if and only if HomD(F–,Y) is representable for all Y in D. Subobject classifier Density theorem Hungerford, Thomas. Algebra. Springer-Verlag. p. 470...

are a cartesian closed category with natural numbers object and subobject classifier, giving rise to the effective topos introduced by Martin Hyland....

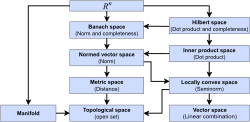
(category theory) Grothendieck topology Introduction to topos theory Subobject classifier Pointless topology Heyting algebra History of category theory Saunders...

If E is a topos, then a topology on E is a morphism j from the subobject classifier Ω to Ω such that j preserves truth ( j ∘ true = true {\displaystyle...

to define a topos is: a properly cartesian closed category with a subobject classifier. Every Grothendieck topos is an elementary topos 1970 John Conway...

global elements of the subobject classifier form a Heyting algebra when ordered by inclusion of the corresponding subobjects of the terminal object....

/B\rightarrow \mathbf {E} /A} which preserves exponentials and the subobject classifier. For any morphism f in E {\displaystyle \mathbf {E} } there is an...

be defined in categorical terms with a morphism s:P × P → Ω, on a subobject classifier (Ω = {0,1} in the category of sets and s(x,y)=1 precisely when x≤y)...

exponential object is given by the ordinal exponentiation nm. The subobject classifier in FinSet and FinOrd is the same as in Set. FinOrd is an example...

in mathematics, which measures when some mathematical object has few subobjects inside it (see for example simple groups, which have no non-trivial normal...

through f. subquotient 1.  A subquotient is a quotient of a subobject. 2.  subobject classifier. subterminal object A subterminal object is an object X such...

the topos has a real numbers object which has no non-trivial decidable subobject. With choice, the notion of Dedekind reals coincides with the Cauchy one...

limit and limit properties but with only a weakened notion of a subobject classifier. Axiom of choice Axiom of countable choice Axiom of replacement History...

logical structure that, if applied to an object, also applies to all subobjects or elements of that object. heterological Describing an adjective that...

d {\displaystyle d} defined on C p + q {\displaystyle C^{p+q}} to the subobject Z r p , q {\displaystyle Z_{r}^{p,q}} . It is straightforward to check...

connection between categorical quantum mechanics and quantum logic, as subobjects in dagger kernel categories and dagger complemented biproduct categories...