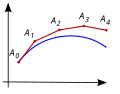
scientific computing, the trapezoidal rule is a numerical method to solve ordinary differential equations derived from the trapezoidal rule for computing integrals...

Eratosthenes Sieve of Sundaram Euler method Backward Euler method Trapezoidal rule (differential equations) Linear multistep methods Runge–Kutta methods Euler integration...

The shallow-water equations (SWE) are a set of hyperbolic partial differential equations (or parabolic if viscous shear is considered) that describe the...

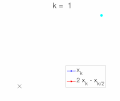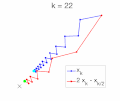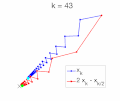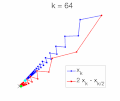
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless...

solving differential equations Lebesgue integration Riemann integral, limit of Riemann sums as the partition becomes infinitely fine Simpson's rule, a powerful...

term is also sometimes used to describe the numerical solution of differential equations. There are several reasons for carrying out numerical integration...

the numerical solution of ordinary differential equations, partial differential equations and integral equations. The idea is to choose a finite-dimensional...

A better approach, the trapezoidal rule, replaces the rectangles used in a Riemann sum with trapezoids. The trapezoidal rule weights the first and last...

Euler method (an explicit method) and the trapezoidal rule (an implicit method). Consider the differential equation y ′ = f ( t , y ) , y ( t 0 ) = y 0 ,...

{\displaystyle y} , so that the differential equation is equivalent to a simple integral, then RK4 is Simpson's rule. The RK4 method is a fourth-order...

In mathematics, specifically the study of differential equations, the Picard–Lindelöf theorem gives a set of conditions under which an initial value problem...

after Karl Heun and is a numerical procedure for solving ordinary differential equations (ODEs) with a given initial value. Both variants can be seen as...

method is based on the trapezoidal rule, giving second-order convergence in time. For linear equations, the trapezoidal rule is equivalent to the implicit...

solving initial value problems. This problem, in which an ordinary differential equation is given together with an initial condition, plays a central role...

rule or the trapezoidal rule. There are various methods for determining the weight coefficients, for example, the Savitzky–Golay filter. Differential...

In mathematics, the Volterra integral equations are a special type of integral equations. They are divided into two groups referred to as the first and...

al-Khwarizmi to include equations of third degree. Like his Arab predecessors, Omar Khayyam provided for quadratic equations both arithmetic and geometric...

for solving differential-algebraic equations (DAEs), i.e., ODEs with constraints: Constraint algorithm — for solving Newton's equations with constraints...

multistep methods are used for the numerical solution of ordinary differential equations. Conceptually, a numerical method starts from an initial point and...

rewritten as y d y = x d x {\displaystyle y\,dy=x\,dx} , which is a differential equation that can be solved by direct integration: ∫ y d y = ∫ x d x , {\displaystyle...

Richardson extrapolation to the trapezoid rule, and the Bulirsch–Stoer algorithm for solving ordinary differential equations. Let A 0 ( h ) {\displaystyle...

substitutions. This is how the supplemental cosine equations are derived from the cosine equations. Similarly, the identities for a quadrantal triangle...

Extreme value theorem Differential equation Differential operator Newton's method Taylor's theorem L'Hôpital's rule General Leibniz rule Mean value theorem...

methods are methods for the numerical solution of the ordinary differential equation d y d t = f ( t , y ) . {\displaystyle {\frac {dy}{dt}}=f(t,y).}...

include the solution to a linear system of equations, the value of an integral, the solution of a differential equation, the minimum of a multivariate function)...

packages that implement the finite element method for solving partial differential equations. This table is contributed by a FEA-compare project, which provides...

with the trapezoidal rule (numerical integration) the most common method. Due to the dependence on the length of x in the trapezoidal rule, the area...

algebraic, differential, discrete and computational geometry. Usually the Cartesian coordinate system is applied to manipulate equations for planes,...

0), is equivalent to the trapezoidal rule with 2n + 1 points; the first extrapolation, R(n, 1), is equivalent to Simpson's rule with 2n + 1 points. The...

which is particularly useful for solving stiff problems and differential-algebraic equations. After spatial discretization, structural dynamics problems...