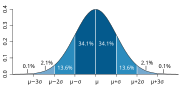
In mathematics, uniform absolute-convergence is a type of convergence for series of functions. Like absolute-convergence, it has the useful property that...

Pointwise absolute-convergence (pointwise convergence of Σ | g k | {\displaystyle \Sigma |g_{k}|} ) Uniform absolute-convergence (uniform convergence of Σ...

space, then local normal convergence (local, uniform, absolute convergence) and compact normal convergence (absolute convergence on compact sets) can be...

In mathematics normal convergence is a type of convergence for series of functions. Like absolute-convergence, it has the useful property that it is preserved...

for convergence to occur. Determination of convergence requires the comprehension of pointwise convergence, uniform convergence, absolute convergence, Lp...

mathematics, convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence or divergence...

of convergence does not coincide with abscissa of absolute convergence. Thus, there might be a strip between the line of convergence and absolute convergence...

only if they are uniformly integrable. This is a generalization of Lebesgue's dominated convergence theorem, see Vitali convergence theorem. Rudin, Walter...

notions of convergence of sequences of random variables, including convergence in probability, convergence in distribution, and almost sure convergence. The...

the power series converges absolutely and uniformly on compact sets inside the open disk of radius equal to the radius of convergence, and it is the Taylor...

power series in complex analysis. Abel's uniform convergence test is a criterion for the uniform convergence of a series of functions dependent on parameters...

|a_{n}|} diverges is said to converge non-absolutely. It is easily shown that absolute convergence of a series implies its convergence. On the other hand, an...

It is a characterization of the convergence in Lp in terms of convergence in measure and a condition related to uniform integrability. Let ( X , A , μ...

a discontinuous pointwise limit. Another notion of convergence is uniform convergence. The uniform distance between two functions f , g : E → R {\displaystyle...

convergence. The early pioneers of functional analysis did not elevate norm convergence above weak convergence and oftentimes viewed weak convergence...

whether they converge or diverge, but also by the properties of the terms an (absolute or conditional convergence); type of convergence of the series...

ƒn(x) = g(x − n). Then, ƒn converges pointwise to 0 but does not converge uniformly to 0. This criterion for uniform convergence is often useful in real...

of this sequence converges in probability to E[f(X,θ)]. This is the pointwise (in θ) convergence. A particular example of a uniform law of large numbers...

M-test. The Cauchy convergence criterion states that a series ∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\infty }a_{n}} converges if and only if the sequence...

topology, topology of G {\displaystyle {\mathcal {G}}} -convergence or topology of uniform convergence on the sets of G {\displaystyle {\mathcal {G}}} is a...

called the disc of convergence of the series. The series converges absolutely inside its disc of convergence, and converges uniformly on every compact subset...

University Press. p. 619. ISBN 978-0-521-54051-3. Lange, K. (1990). "Convergence of Image Reconstruction Algorithms with Gibbs Smoothing". IEEE Trans...

numbers, it does converge to the irrational number 2 {\displaystyle {\sqrt {2}}} . The open interval (0,1), again with the absolute difference metric...

proved that the convergence in law of Gn to the Brownian bridge holds for Uniform[0,1] distributions with respect to uniform convergence in t over the interval...

integral of the absolute value of the difference between the densities. Convergence in total variation is stronger than weak convergence. An important example...

convergence, Uniform convergence Absolute convergence, Conditional convergence Normal convergence Radius of convergence Integral test for convergence...

analogous statement for convergence of improper integrals is proven using integration by parts. If the integral of a function f is uniformly bounded over all...

assumptions, the Tweedie convergence theorem would imply that Taylor's law results from a general mathematical convergence effect much as how the central...

_{j=1}^{\infty }\lambda _{j}\,e_{j}(s)\,e_{j}(t)} where the convergence is absolute and uniform. We now explain in greater detail the structure of the proof...

indicate, weak convergence is weaker than strong convergence. In fact, strong convergence implies convergence in probability, and convergence in probability...