In mathematics, Wedderburn's little theorem states that every finite division ring is a field; thus, every finite domain is a field. In other words, for...

commutative, is called a division ring (or sometimes skew field). By Wedderburn's little theorem, any finite division ring is commutative, and hence is a finite...

multiplication is not required to be commutative. However, by Wedderburn's little theorem all finite division rings are commutative and therefore finite...

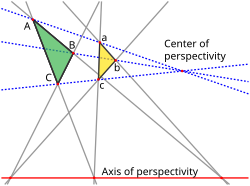
facts (rather than the full strength of Wedderburn's little theorem). The ten lines involved in Desargues's theorem (six sides of triangles, the three lines...

have a b–1 ≠ b–1 a. A commutative division ring is a field. Wedderburn's little theorem asserts that all finite division rings are commutative and therefore...

Wedderburn's theorem may refer to: Artin–Wedderburn theorem, classifying semisimple rings and semisimple algebras Wedderburn's theorem on simple rings...

This follows from two theorems of Joseph Wedderburn established in 1905 and 1907 (one of which is Wedderburn's little theorem). In 1964 David Singmaster...

that a finite division algebra is a field (Wedderburn's little theorem), and part of the Artin–Wedderburn theorem on simple algebras. He also worked on group...

finite division ring) is a field; in particular commutative (the Wedderburn's little theorem). Every module over a division ring is a free module (has a basis);...

theorem (ring theory) Regev's theorem (ring theory) Skolem–Noether theorem (simple algebras) Wedderburn's little theorem (ring theory) Wedderburn's theorem...

of Wedderburn's Theorem". American Mathematical Monthly. 71 (6): 652–653. doi:10.2307/2312328. JSTOR 2312328. A proof of Wedderburn's little theorem in...

complex numbers (dimension 2), and the quaternions (dimension 4). Wedderburn's little theorem states that if D is a finite division algebra, then D is a finite...

is prime. A finite domain is automatically a finite field, by Wedderburn's little theorem. The quaternions form a noncommutative domain. More generally...

module categories Cartan–Brauer–Hua theorem gives insight on the structure of division rings Wedderburn's little theorem states that finite domains are fields...

topology in 1958 by Michel Kervaire, Raoul Bott, and John Milnor. Wedderburn's little theorem states that all finite division rings are fields. The a priori...

divisors. A finite ring with no zero divisors is a field by Wedderburn's little theorem, but there is no field with ten elements because every finite...

postulate Fermat's theorem on sums of two squares Two proofs of the Law of quadratic reciprocity Proof of Wedderburn's little theorem asserting that every...

Bamberg, John; Penttila, Tim (2015), "Completing Segre's proof of Wedderburn's little theorem" (PDF), Bulletin of the London Mathematical Society, 47 (3):...

what he did are unclear. Leech lattice Verschiebung operator Wedderburn's little theorem List of things named after Ernst Witt Kersten, Ina (20 October...

If D is finite then it must be a finite field GF(q), since by Wedderburn's little theorem all finite division rings are fields. In this case, this construction...

finite integral domains are finite fields (more generally, by Wedderburn's little theorem, finite domains are finite fields). The ring of integers Z {\displaystyle...

ideal theorem Levitzky's theorem Galois theory Abel–Ruffini theorem Artin-Wedderburn theorem Jacobson density theorem Wedderburn's little theorem Lasker–Noether...

begins with Witt’s formulation of Wedderburn’s proof that a finite division ring is commutative ('Wedderburn's little theorem'). Properties of Haar measure...

but, believing Wedderburn's first proof to be correct, Dickson acknowledged Wedderburn's priority. But Dickson also noted that Wedderburn constructed his...

ISBN 978-1-4704-2849-5. Dudley 1978, Theorem 3, p. 28. Shahriari 2017, pp. 27–28. Ribenboim 2004, Fermat's little theorem and primitive roots modulo a prime...

1907 Wedderburn extended Cartan's results to an arbitrary field, in what are now called the Wedderburn principal theorem and Artin–Wedderburn theorem. For...

satisfy the above equation which can be deduced from Fermat's little theorem. Fermat's theorem asserts that if p is prime, and coprime to a, then ap−1 ≡ 1...

important class of pseudoprimes that come from Fermat's little theorem. Fermat's little theorem states that if p {\displaystyle p} is prime and a {\displaystyle...

where the strict converse of Fermat's Little Theorem does not hold. This fact precludes the use of that theorem as an absolute test of primality. The...

where 23 = 1 + (2 × 11) and 89 = 1 + 4 × (2 × 11). Proof: By Fermat's little theorem, q is a factor of 2q−1 − 1. Since q is a factor of 2p − 1, for all positive...