In mathematics, a binary relation R is called well-founded (or wellfounded or foundational) on a set or, more generally, a class X if every non-empty...

a non-strict well ordering, then < is a strict well ordering. A relation is a strict well ordering if and only if it is a well-founded strict total order...

i<j.} Well-founded induction can be used on any set with a well-founded relation, thus one is interested in when a quasi-order is well-founded. (Here...

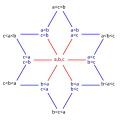
In mathematics, a binary relation R on a set X is transitive if, for all elements a, b, c in X, whenever R relates a to b and b to c, then R also relates...

mathematics, an equivalence relation is a binary relation that is reflexive, symmetric, and transitive. The equipollence relation between line segments in...

whose value is monotonically decreased with respect to a (strict) well-founded relation by the iteration of a while loop under some invariant conditions...

transfinite recursion on any well-founded relation R. (R need not even be a set; it can be a proper class, provided it is a set-like relation; i.e. for any x, the...

well-foundedness. In non-well-founded set theories, the foundation axiom of ZFC is replaced by axioms implying its negation. The study of non-well-founded...

binary relation associates some elements of one set called the domain with some elements of another set called the codomain. Precisely, a binary relation over...

In mathematics, a binary relation R {\displaystyle R} on a set X {\displaystyle X} is antisymmetric if there is no pair of distinct elements of X {\displaystyle...

from the domain of a well-founded relation, such as from the ordinal numbers. If the measure "decreases" according to the relation along every possible...

reflexive relation is the relation "is equal to" on the set of real numbers, since every real number is equal to itself. A reflexive relation is said to...

mathematics, especially in order theory, a preorder or quasiorder is a binary relation that is reflexive and transitive. The name preorder is meant to suggest...

and reflexive relation on X {\displaystyle X} ) that is strongly connected (meaning that any two points are comparable) and well-founded in the sense that...

A symmetric relation is a type of binary relation. Formally, a binary relation R over a set X is symmetric if: ∀ a , b ∈ X ( a R b ⇔ b R a ) , {\displaystyle...

which any two elements are comparable. That is, a total order is a binary relation ≤ {\displaystyle \leq } on some set X {\displaystyle X} , which satisfies...

In mathematics, an asymmetric relation is a binary relation R {\displaystyle R} on a set X {\displaystyle X} where for all a , b ∈ X , {\displaystyle...

the latter (→) is moreover well-founded, it is called a reduction ordering, or a reduction preorder. Given a binary relation R, its rewrite closure is...

pair is comparable. Formally, a partial order is a homogeneous binary relation that is reflexive, antisymmetric, and transitive. A partially ordered set...

the transitive closure R+ of a homogeneous binary relation R on a set X is the smallest relation on X that contains R and is transitive. For finite sets...

{\displaystyle \in } -well-founded. For a binary relation R D {\displaystyle R_{D}} on a set D {\displaystyle D} , well-foundedness can be defined by requiring...

binary relation is the relation that occurs when the order of the elements is switched in the relation. For example, the converse of the relation 'child of'...

ccc Knaster's condition, sometimes denoted property (K) Well-founded relation Ordinal number Well-quasi-ordering Semilattice Lattice (Directed) complete...

either relation (union), removing tuples from the first relation found in the second relation (difference), extending the tuples of the first relation with...

In mathematics, a binary relation R ⊆ X×Y between two sets X and Y is total (or left total) if the source set X equals the domain {x : there is a y with...

the covering relation of a partially ordered set, independently of any drawing of that graph. Although Hasse diagrams are simple, as well as intuitive...

(strictly partially ordered sets in which incomparability is a transitive relation), as total preorders (transitive binary relations in which at least one...

mathematics, especially order theory, the covering relation of a partially ordered set is the binary relation which holds between comparable elements that are...

respect to the associated ordering relation. For an explanation see the entry preservation of limits. There is a well-known equivalence between the category...

also have to show that the loop terminates. For this we define a well-founded relation on the state space denoted as (wfs, <) and define a variant function...