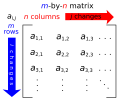
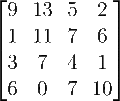an invertible matrix (non-singular, non-degenerate or regular) is a square matrix that has an inverse. In other words, if a matrix is invertible, it...

general linear group of all invertible matrices. A triangular matrix is invertible precisely when its diagonal entries are invertible (non-zero). Over the real...

matrix A {\displaystyle A}  is called diagonalizable or non-defective if it is similar to a diagonal matrix. That is, if there exists an invertible matrix...

element is invertible under addition). Inverses are commonly used in groups—where every element is invertible, and rings—where invertible elements are...

m\times n} matrix A {\displaystyle A} . A square matrix A {\displaystyle A} is called invertible or non-singular if there exists a matrix B {\displaystyle...

invertible matrices is again invertible, and the inverse of an invertible matrix is invertible, with the identity matrix as the identity element of the...

identity matrix. Involutory matrices are all square roots of the identity matrix. This is a consequence of the fact that any invertible matrix multiplied...

A singular matrix is a square matrix that is not invertible, unlike non-singular matrix which is invertible. Equivalently, an n {\displaystyle n} -by-...

an invertible matrix B {\displaystyle B} with conjugate transpose B ∗ {\displaystyle B^{*}} such that M = B ∗ B . {\displaystyle M=B^{*}B.} A matrix is...

,} where I is the identity matrix of the same size as A. Consequently, the multiplicative inverse of an invertible matrix can be found by dividing its...

in particular linear algebra, the matrix determinant lemma computes the determinant of the sum of an invertible matrix A and the dyadic product, u vT, of...

defined using the Leibniz formula; such a matrix is invertible if and only if its determinant is invertible in R, generalizing the situation over a field...

{T} }=Q^{-1},} where Q−1 is the inverse of Q. An orthogonal matrix Q is necessarily invertible (with inverse Q−1 = QT), unitary (Q−1 = Q∗), where Q∗ is the...

words, the matrix of the combined transformation A followed by B is simply the product of the individual matrices. When A is an invertible matrix there is...

The transpose of an invertible matrix is also invertible, and its inverse is the transpose of the inverse of the original matrix. The notation A−T is...

{2}}\end{bmatrix}}.} An invertible matrix A is a generalized permutation matrix if and only if it can be written as a product of an invertible diagonal matrix D and an...

Invertible may refer to Invertible element Invertible function Invertible ideal Invertible knot Invertible jet Invertible matrix Invertible module Invertible...

inverse of a "rank-1 update" to a matrix whose inverse has previously been computed. That is, given an invertible matrix A {\displaystyle A} and the outer...

represented, on a given basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the corresponding linear map...

\dots ,\ x_{n}} are distinct, then V is a square matrix with non-zero determinant, i.e. an invertible matrix. Thus, given V and y, one can find the required...

an invertible matrix. Most rotation matrices fit this description, and for them it can be shown that (Q − I)(Q + I)−1 is a skew-symmetric matrix, A....

Neumann series can be used for approximate matrix inversion. To approximate the inverse of an invertible matrix A {\displaystyle A} , consider that A − 1...

the inverse of an invertible matrix. The method is named after Carl Friedrich Gauss (1777–1855). To perform row reduction on a matrix, one uses a sequence...

{\begin{bmatrix}B\\\hline C\end{bmatrix}}} means that there exists an invertible matrix P {\displaystyle P} such that [ A I ] P = [ B C ] , {\displaystyle...

matrix similarity. The row echelon form is a canonical form, when one considers as equivalent a matrix and its left product by an invertible matrix....

of a Lie algebra, when the Lie algebra is gln Invertible matrix (this usage is rare) QS Regular Matrix, a quadraphonic sound system developed by Sansui...

In linear algebra, an invertible complex square matrix U is unitary if its matrix inverse U−1 equals its conjugate transpose U*, that is, if U ∗ U = U...

=\mathbf {I} .} A matrix that has an inverse is an invertible matrix. Otherwise, it is a singular matrix. A product of matrices is invertible if and only if...

diagonal matrix is invertible if and only if each of its main-diagonal blocks are invertible, and in this case its inverse is another block diagonal matrix given...

subgroup of upper triangular invertible matrices, so Bruhat decomposition says that one can write any invertible matrix A {\displaystyle A} as a product...