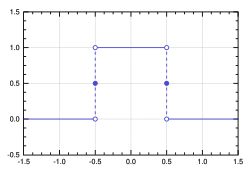
mathematical analysis, the Dirac delta function (or δ distribution), also known as the unit impulse, is a generalized function on the real numbers, whose...

}\delta (t-kT)} for some given period T {\displaystyle T} . Here t is a real variable and the sum extends over all integers k. The Dirac delta function...

continuous-time systems the Dirac delta function is often confused for both the Kronecker delta function and the unit sample function. The Dirac delta is defined as:...

of formalizing the idea of the Dirac delta function, an important tool in physics and other technical fields. A Dirac measure is a measure δx on a set...

function contains all frequencies (see the Fourier transform of the Dirac delta function, showing infinite frequency bandwidth that the Dirac delta function...

quantum mechanics the delta potential is a potential well mathematically described by the Dirac delta function - a generalized function. Qualitatively, it...

as points with non-zero charge). The Dirac delta function, or δ function, is (informally) a generalized function on the real number line that is zero...

Green's function G {\displaystyle G} is the solution of the equation L G = δ {\displaystyle LG=\delta } , where δ {\displaystyle \delta } is Dirac's delta function;...

integral of the Dirac delta function. This is sometimes written as H ( x ) := ∫ − ∞ x δ ( s ) d s {\displaystyle H(x):=\int _{-\infty }^{x}\delta (s)\,ds} although...

{\displaystyle \delta (t)} is δ ( f ) = 1 , {\displaystyle \delta (f)=1,} means that the frequency spectrum of the Dirac delta function is infinitely broad...

on the indicator function of some domain D. It is a generalisation of the derivative (or "prime function") of the Dirac delta function to higher dimensions;...

continuity in his Cours d'Analyse, and in defining an early form of a Dirac delta function. As Cantor and Dedekind were developing more abstract versions of...

1920s and 1930s further basic steps were taken. The Dirac delta function was boldly defined by Paul Dirac (an aspect of his scientific formalism); this was...

arguments. The integral of the Dirac delta function. Sawtooth wave Square wave Triangle wave Rectangular function Floor function: Largest integer less than...

in distribution theory, the derivative of the signum function is two times the Dirac delta function. This can be demonstrated using the identity sgn ⁡ x...

career, Dirac made numerous important contributions to mathematical subjects, including the Dirac delta function, Dirac algebra and the Dirac operator...

non-existent Dirac delta function). However, there are RKHSs in which the norm is an L2-norm, such as the space of band-limited functions (see the example...

A Dirac delta function or simply delta function is a generalized function on the real number line denoted by δ that is zero everywhere except at zero...

distribution becomes a one-point degenerate distribution with a Dirac delta function spike at the right end, x = 1, with probability 1, and zero probability...

variance as a generalized function; specifically, as a Dirac delta function ⁠ δ {\displaystyle \delta } ⁠ translated by the mean ⁠ μ {\displaystyle \mu }...

The Kronecker delta in mathematics. The central difference for a function. The degree of a vertex in graph theory. The Dirac delta function in mathematics...

three-dimensional space, and δ {\displaystyle \delta } is the Dirac delta function. The algebraic expression of the Green's function for the three-variable Laplace operator...

the step response to a step input, or the impulse response to a Dirac delta function input. In the frequency domain (for example, looking at the Fourier...

magnetic field is proportional to the Dirac delta function at the origin. We must define one set of functions for the vector potential on the "northern...

potentials that are not functions but are distributions, such as the Dirac delta function. It is easy to visualize a sequence of functions meeting the requirement...

provides an exact solution to the quantum-mechanical double-well Dirac delta function model for equal charges—a fundamental problem in physics. Prompted...

functions. Symmetric function: value is independent of the order of its arguments Generalized function: a wide generalization of Dirac delta function...

distributions, which gives a well-defined meaning to objects such as the Dirac delta function. He was awarded the Fields Medal in 1950 for his work on the theory...

step function is equal to the Dirac delta function, i.e. d H ( x ) d x = δ ( x ) {\displaystyle {\frac {\mathrm {d} H(x)}{\mathrm {d} x}}=\delta (x)}...

A Dirac pulse has the shape of the Dirac delta function. It has the properties of infinite amplitude and its integral is the Heaviside step function. Equivalently...