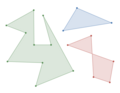
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either...
58 KB (7,173 words) - 01:04, 1 July 2025
Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science. In computational geometry...
17 KB (2,326 words) - 04:22, 2 May 2025
subset A of Euclidean space is called the convex hull of A. It is the smallest convex set containing A. A convex function is a real-valued function defined...
27 KB (3,429 words) - 17:52, 10 May 2025
Carathéodory's theorem is a theorem in convex geometry. It states that if a point x {\displaystyle x} lies in the convex hull C o n v ( P ) {\displaystyle \mathrm...
15 KB (2,341 words) - 19:31, 25 June 2025
locally convex space, the convex hull and the disked hull of a totally bounded set is totally bounded. In a complete locally convex space, the convex hull and...
58 KB (10,568 words) - 04:52, 2 July 2025
learning resources about Convex combination Affine hull Carathéodory's theorem (convex hull) Simplex Barycentric coordinate system Convex space Rockafellar,...
7 KB (542 words) - 18:16, 1 January 2025
"balanced"), in which case it is called a disk. The disked hull or the absolute convex hull of a set is the intersection of all disks containing that set...
11 KB (1,913 words) - 09:38, 28 August 2024
the convex hull of its edges. Additional properties of convex polygons include: The intersection of two convex polygons is a convex polygon. A convex polygon...
6 KB (881 words) - 09:02, 13 March 2025
every convex set is orthogonally convex but not vice versa. For the same reason, the orthogonal convex hull itself is a subset of the convex hull of the...
13 KB (1,508 words) - 09:50, 5 March 2025
The dynamic convex hull problem is a class of dynamic problems in computational geometry. The problem consists in the maintenance, i.e., keeping track...
6 KB (769 words) - 22:54, 28 July 2024
and computational geometry, the relative convex hull or geodesic convex hull is an analogue of the convex hull for the points inside a simple polygon or...
9 KB (1,112 words) - 11:33, 27 May 2025
spheres determines a specific volume known as the convex hull of the packing, defined as the smallest convex set that includes all the spheres. There are many...
16 KB (2,655 words) - 20:49, 19 June 2025
A kinetic convex hull data structure is a kinetic data structure that maintains the convex hull of a set of continuously moving points. It should be distinguished...
12 KB (1,934 words) - 20:41, 10 November 2022
Polyhedron (redirect from Convex polyhedra)
The convex polyhedra are a well defined class of polyhedra with several equivalent standard definitions. Every convex polyhedron is the convex hull of...
96 KB (10,656 words) - 22:12, 1 July 2025
Function of several complex variables (redirect from Holomorphically convex hull)
The polynomially convex hull contains the holomorphically convex hull. The domain G {\displaystyle G} is called holomorphically convex if for every compact...
124 KB (17,717 words) - 22:01, 1 July 2025
C} is the convex hull of its extremal rays. For a vector space V {\displaystyle V} , every linear subspace of V {\displaystyle V} is a convex cone. In...
28 KB (3,941 words) - 12:49, 8 May 2025
In discrete geometry and computational geometry, the convex hull of a simple polygon is the polygon of minimum perimeter that contains a given simple...
9 KB (1,141 words) - 03:36, 2 June 2025
convex set of points in space. Other important definitions are: as the intersection of half-spaces (half-space representation) and as the convex hull...
23 KB (3,262 words) - 04:00, 7 July 2025
Delone triangulation of a set of points in the plane subdivides their convex hull into triangles whose circumcircles do not contain any of the points;...
29 KB (3,255 words) - 08:43, 18 June 2025
Local convex hull (LoCoH) is a method for estimating size of the home range of an animal or a group of animals (e.g. a pack of wolves, a pride of lions...
7 KB (1,116 words) - 14:30, 8 June 2025
Krein–Milman theorem (category Convex hulls)
to the closed convex hull of its extreme points. This theorem generalizes to infinite-dimensional spaces and to arbitrary compact convex sets the following...
20 KB (2,957 words) - 18:17, 16 April 2025
problems, including point in polygon testing, area computation, the convex hull of a simple polygon, triangulation, and Euclidean shortest paths. Other...
31 KB (3,206 words) - 07:42, 13 March 2025
Alpha shape (category Convex hulls)
generalization of the concept of the convex hull, i.e. every convex hull is an alpha-shape but not every alpha shape is a convex hull. For each real number α, define...
6 KB (720 words) - 16:27, 2 March 2025
geometric object that was discovered by Paul Schatz in 1929. It is the convex hull of a skeletal frame made by placing two linked congruent circles in perpendicular...
8 KB (972 words) - 15:06, 30 May 2025
Olshevsky nicknamed it the yog-sothoth (after the Cthulhu Mythos deity). Its convex hull is a nonuniform truncated dodecahedron. Let ξ = − 3 2 − 1 2 1 + 4 ϕ ≈...
4 KB (576 words) - 12:15, 27 June 2024
Closed hulls In a locally convex space, convex hulls of bounded sets are bounded. This is not true for TVSs in general. The closed convex hull of a set...
103 KB (13,546 words) - 12:16, 1 May 2025
Quickhull (redirect from Quick hull)
Quickhull is a method of computing the convex hull of a finite set of points in n-dimensional space. It uses a divide and conquer approach similar to...
8 KB (1,052 words) - 19:00, 28 April 2025
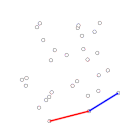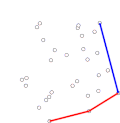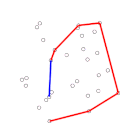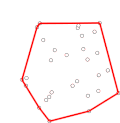
Graham scan (category Convex hull algorithms)
Graham's scan is a method of finding the convex hull of a finite set of points in the plane with time complexity O(n log n). It is named after Ronald...
12 KB (1,738 words) - 04:24, 11 February 2025
Gift wrapping algorithm (category Convex hull algorithms)
geometry, the gift wrapping algorithm is an algorithm for computing the convex hull of a given set of points. In the two-dimensional case the algorithm is...
5 KB (680 words) - 12:25, 19 June 2024
when c lies in the interior of the convex hull of S, and otherwise (when c lies on the boundary of the convex hull of S) A is unbounded. A subset F of...
11 KB (1,578 words) - 11:34, 28 May 2024