mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds...
20 KB (3,890 words) - 13:36, 13 April 2025
In many-body physics, the problem of analytic continuation is that of numerically extracting the spectral density of a Green function given its values...
8 KB (1,027 words) - 15:50, 3 February 2025
Monodromy theorem (redirect from Analytic continuation along a curve)
important result about analytic continuation of a complex-analytic function to a larger set. The idea is that one can extend a complex-analytic function (from...
8 KB (1,331 words) - 14:39, 17 November 2023
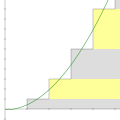
Divergent series (section Analytic continuation)
arithmetic mean of the sequence of partial sums. Other methods involve analytic continuations of related series. In physics, there are a wide variety of summability...
32 KB (5,028 words) - 15:28, 17 May 2025
zeta function is that it can be defined for other values of s by analytic continuation. One can then define the zeta-regularized sum of 1 + 2 + 3 + 4 +...
33 KB (4,219 words) - 07:38, 20 May 2025
Complex analysis (redirect from Theory of analytic functions)
the principle of analytic continuation which allows extending every real analytic function in a unique way for getting a complex analytic function whose...
18 KB (2,538 words) - 09:09, 12 May 2025
an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions...
16 KB (2,233 words) - 20:48, 31 March 2025
Gamma function (section Analytic number theory)
The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic function which is...
90 KB (13,517 words) - 19:06, 28 March 2025
naturally in considering the possible analytic continuations of an analytic function, since analytic continuations may have a non-trivial monodromy. They...
2 KB (294 words) - 16:45, 12 February 2021
product expansion, it satisfies a functional equation, it has an analytic continuation to a meromorphic function on the complex plane C with only a simple...
11 KB (1,594 words) - 21:30, 7 February 2025
analysis, such as holomorphicity, the theory of algebraic curves, and analytic continuation. However, the numerical implementation is rather straightforward...
18 KB (2,491 words) - 11:59, 9 February 2025
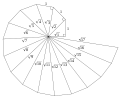
{\displaystyle f(0)=1,} and monotonicity in both argument and modulus. An analytic continuation of Davis' continuous form of the Spiral of Theodorus extends in...
10 KB (1,156 words) - 22:04, 19 April 2025
Geometric function theory (category Analytic functions)
function is conformal. Analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining...
13 KB (1,787 words) - 15:31, 22 January 2024
differentiable functions) and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument...
14 KB (2,056 words) - 00:01, 24 December 2024
{\displaystyle z} . Here the branch point is the origin, because the analytic continuation of any solution around a closed loop containing the origin will...
17 KB (2,729 words) - 18:14, 14 June 2024
titled "On Integral Equations, Their Solution by Iteration and Analytic Continuation". In 1952, he participated in Project Whirlwind. He joined the faculty...
8 KB (668 words) - 17:42, 27 April 2025
{1}{1-z}}} which converges in the larger region Re(z) < 1, giving an analytic continuation of the original series. Considering instead the weak Borel transform...
22 KB (3,525 words) - 21:16, 14 April 2025
convergent on a half-plane, that may give rise to an L-function via analytic continuation. The Riemann zeta function is an example of an L-function, and some...
8 KB (984 words) - 11:59, 7 May 2024
explicit in complex analysis. In the process of analytic continuation, a function that is an analytic function F ( z ) {\displaystyle F(z)} in some open...
11 KB (1,692 words) - 09:54, 17 May 2025
these points as branch points. The sum of these functions gives the analytic continuation of the bilateral hypergeometric series to all values of z other...
5 KB (1,001 words) - 07:50, 27 September 2023
In physics, a wave packet (also known as a wave train or wave group) is a short burst of localized wave action that travels as a unit, outlined by an envelope...
39 KB (5,959 words) - 18:46, 15 May 2025
Function of several complex variables (redirect from The theory of analytic functions of several complex variables)
theory. A number of issues were clarified, in particular that of analytic continuation. Here a major difference is evident from the one-variable theory;...
124 KB (17,717 words) - 09:54, 7 April 2025
p-adic analytic manifolds, rigid analytic spaces admit meaningful notions of analytic continuation and connectedness. The basic rigid analytic object...
8 KB (991 words) - 19:19, 12 March 2025
respect to z at every point of U. Equivalently, it is holomorphic if it is analytic, that is, if its Taylor series exists at every point of U, and converges...
9 KB (1,479 words) - 11:37, 3 May 2025
Riemann zeta function (category Analytic number theory)
\operatorname {Re} (s)>1} , and its analytic continuation elsewhere. The Riemann zeta function plays a pivotal role in analytic number theory and has applications...
74 KB (10,674 words) - 01:04, 20 April 2025
Complex logarithm (category Analytic functions)
integration of 1 / z {\displaystyle 1/z} , or by the process of analytic continuation. There is no continuous complex logarithm function defined on all...
30 KB (4,831 words) - 06:58, 24 March 2025
0, it follows that g' (z)/g(z) has no singularities at zZ, and thus is analytic at zZ, which implies that the residue of f′(z)/f(z) at zZ is k. Let zP...
9 KB (1,612 words) - 18:24, 30 March 2025
originated in complex analysis, from analytic continuation. It often occurs that one knows the value of a complex analytic function f ( z ) {\displaystyle...
11 KB (1,432 words) - 14:44, 16 May 2025
complex functions, typically analytic functions. The domain to which a complex function may be extended by analytic continuation generally consists of almost...
76 KB (11,411 words) - 01:25, 21 May 2025
of definition of a complex analytic function, i.e., it is a form of analytic continuation. It states that if an analytic function is defined on the upper...
3 KB (344 words) - 06:41, 7 January 2024