differentiable, so are holomorphic functions (this is in contrast to the case of real differentiable functions), and the fact that the radius of convergence is...

theorem in complex analysis. Holomorphic functions are also sometimes referred to as regular functions. A holomorphic function whose domain is the whole...

functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do...

concerned with analytic functions of a complex variable, that is, holomorphic functions. The concept can be extended to functions of several complex...

this class of functions. In several ways, the harmonic functions are real analogues to holomorphic functions. All harmonic functions are analytic, that is...

in complex analysis of functions of one variable, which is the case n = 1, the functions studied are holomorphic or complex analytic so that, locally, they...

line integrals for holomorphic functions in the complex plane. Essentially, it says that if f ( z ) {\displaystyle f(z)} is holomorphic in a simply connected...

theory of holomorphic functions is a division of mathematical analysis. The purpose of the theory is to provide quantitative measures of the number of times...

proved that holomorphic functions are analytic and analytic complex functions are complex-differentiable. In particular, holomorphic functions are infinitely...

expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral...

holomorphy is a branch of functional analysis. It is concerned with generalizations of the concept of holomorphic function to functions defined and taking...

In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just...

point of U. Equivalently, it is holomorphic if it is analytic, that is, if its Taylor series exists at every point of U, and converges to the function in...

can be used to express holomorphic functions defined on an annulus, much as power series are used to express holomorphic functions defined on a disc. Suppose...

mathematics, smooth functions (also called infinitely differentiable functions) and analytic functions are two very important types of functions. One can easily...

is the derivative of the holomorphic function F, it is holomorphic. The fact that derivatives of holomorphic functions are holomorphic can be proved by...

antiholomorphic functions (also called antianalytic functions) are a family of functions closely related to but distinct from holomorphic functions. A function of the...

\{a_{k}\}_{k}\rightarrow \mathbb {C} } that is holomorphic except at the discrete points {ak}k, even if some of them are essential singularities.) Residues...

is holomorphic except at zero and the negative integers, where it has simple poles. The gamma function has no zeros, so the reciprocal gamma function ⁠1/Γ(z)⁠...

lemma is a result in complex analysis typically viewed to be about holomorphic functions from the open unit disk D := { z ∈ C : | z | < 1 } {\displaystyle...

Proof that holomorphic functions are analytic. The infinite product for Γ(z) is uniformly convergent on any bounded region where none of its denominators...

exponential function is a holomorphic function with a nonzero derivative, but is not one-to-one since it is periodic. The Riemann mapping theorem, one of the...

analytic functions, unlike for complex analytic (that is, holomorphic) functions, these statements fail to hold. For example, consider the function f...

boundary, the normal derivative of φ is zero. Solutions of Laplace's equation are called harmonic functions; they are all analytic within the domain where the...

properties of the modular lambda function, usually denoted by λ {\textstyle \lambda } , and which performs, using modern terminology, the holomorphic universal...

Hardy space consisting of the closure in L2(∂D) of all holomorphic functions in D continuous up to the boundary of D. Then functions in H2(∂D) uniquely extend...

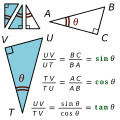
trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled...

Lars (1979). Complex analysis: an introduction to the theory of analytic functions of one complex variable. McGraw-Hill. ISBN 978-0-07-000657-7. Churchill...

dy} which is an analytic function. Note that the foregoing proof of analyticity derived an expression for a system of n different function elements fi (x)...

approximates any holomorphic function arbitrarily well. Since holomorphic functions are very general, this property is quite remarkable. The first proof of universality...