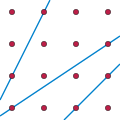
geometry, Beck's theorem is any of several different results, two of which are given below. Both appeared, alongside several other important theorems...

Mock Beck, on monadic functors in category theory Beck's theorem (geometry) (1983) by József Beck, on finite collections of points in discrete geometry This...

In geometry, Pick's theorem provides a formula for the area of a simple polygon with integer vertex coordinates, in terms of the number of integer points...

branch of mathematics, Beck's monadicity theorem gives a criterion that characterises monadic functors, introduced by Jonathan Mock Beck (2003) in about 1964...

with 0.42. The Szemerédi–Trotter theorem has a number of consequences, including Beck's theorem in incidence geometry and the Erdős-Szemerédi sum-product...

enumerate the lattice points in some convex bodies. In the geometry of numbers, the subspace theorem was obtained by Wolfgang M. Schmidt in 1972. It states...

bisector theorem (Euclidean geometry) Anne's theorem (geometry) Apollonius's theorem (plane geometry) Barbier's theorem (geometry) Beck's theorem (incidence...

in terms of the implicit constants. This result can be used to prove Beck's theorem. A similar bound for the number of incidences is conjectured for point-circle...

The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the...

3295, MR 1932078, S2CID 8136773. Beck, Matthias; Zaslavsky, Thomas (2003), "A Meshalkin theorem for projective geometries", Journal of Combinatorial Theory...

theory in his 1990 paper for the "Grothendieck Festschrift", employing Beck's theorem – the Tannakian category concept being the categorical expression of...

ISBN 978-0-521-46300-3. MR 1462892. Nikolayevsky, Y. (2003). "Two theorems on Osserman manifolds". Differential Geometry and Its Applications. 18 (3): 239–253. doi:10...

algebraic geometry were not). From the point of view of abstract category theory the work of comonads of Beck was a summation of those ideas; see Beck's monadicity...

In combinatorics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colours)...

made extensive use of it in treating foundational aspects of algebraic geometry. Outside that field, it has been influential particularly on category theory...

Bruijn–Erdős theorem (graph theory) de Bruijn–Erdős theorem (incidence geometry) Davenport–Erdős theorem Erdős–Anning theorem Erdős–Beck theorem Erdős–Dushnik–Miller...

theorems: Geometric discrepancy theory The theorem of van Aardenne-Ehrenfest Arithmetic progressions (Roth, Sarkozy, Beck, Matousek & Spencer) Beck–Fiala...

of lines, an impossibility. The inequality can also be used to prove Beck's theorem, that if a finite point set does not have a linear number of collinear...

the Beck–Fiala theorem in discrepancy theory, the algorithmic version of the Lovász local lemma, the two extremes theorem in combinatorial geometry and...

In geometry, the Minkowski sum of two sets of position vectors A and B in Euclidean space is formed by adding each vector in A to each vector in B: A +...

version of Beck's theorem, characterizing comonadic adjunctions, is relevant in different fields such as topos theory and topics in algebraic geometry related...

matrix. 1985: Jozsef Beck for tight bounds on the discrepancy of arithmetic progressions. H. W. Lenstra Jr. for using the geometry of numbers to solve...

presentation). A faithfully flat descent is a special case of Beck's monadicity theorem. Given a faithfully flat ring homomorphism A → B {\displaystyle...

Japanese and American mathematician, best known for his eponymous fixed-point theorem. Kakutani attended Tohoku University in Sendai, where his advisor was Tatsujirō...

properness Chevalley group Chevalley scheme Chevalley–Iwahori–Nagata theorem Beck–Chevalley condition Non-conformist movement Jordan–Chevalley decomposition...

structures. Matroid Greedoid Ramsey theory Van der Waerden's theorem Hales–Jewett theorem Umbral calculus, binomial type polynomial sequences Combinatorial...

In differential geometry, the Carathéodory conjecture is a mathematical conjecture attributed to Constantin Carathéodory by Hans Ludwig Hamburger in a...

polynomials can be seen as a higher-dimensional generalization of Pick's theorem in the Euclidean plane. These polynomials are named after Eugène Ehrhart...

104–119. Beck, Matthias; Pixton, Dennis (1 October 2003), "The Ehrhart Polynomial of the Birkhoff Polytope", Discrete and Computational Geometry, 30 (4):...

In elementary geometry, a polytope is a geometric object with flat sides (faces). Polytopes are the generalization of three-dimensional polyhedra to any...