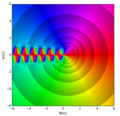
In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function: ψ ( z ) = d d z ln ⁡ Γ ( z ) = Γ ′ ( z ) Γ ( z )...

{\Gamma '(z)}{\Gamma (z)}}} holds where ψ(z) is the digamma function and Γ(z) is the gamma function. They are holomorphic on C ∖ Z ≤ 0 {\displaystyle \mathbb...

{\displaystyle \psi _{1}(z)={\frac {d}{dz}}\psi (z)} where ψ(z) is the digamma function. It may also be defined as the sum of the series ψ 1 ( z ) = ∑ n =...

the digamma function. Therefore, the geometric mean of a beta distribution with shape parameters α and β is the exponential of the digamma functions of...

Digamma or wau (uppercase: Ϝ, lowercase: ϝ, numeral: ϛ) is an archaic letter of the Greek alphabet. It originally stood for the sound /w/ but it has remained...

of the gamma function is called the digamma function; higher derivatives are the polygamma functions. The analog of the gamma function over a finite...

1\leq m\leq n,} where ψ ( z ) {\displaystyle \psi (z)} denotes the digamma function. Stirling's approximation gives the asymptotic formula B ( x , y )...

where ψ ( z ) {\displaystyle \psi (z)} is the digamma function, the logarithmic derivative of the gamma function. There is also a corresponding integral formula...

gamma function insofar as the latter is obtained by a particular choice of multivariate argument of the former. We may define the multivariate digamma function...

coefficient analogue. Digamma function, Polygamma function Incomplete beta function Incomplete gamma function K-function Multivariate gamma function: A generalization...

numbers, but this remains unproven. The digamma function is defined as the logarithmic derivative of the gamma function ψ ( x ) = d d x ln ⁡ ( Γ ( x ) ) =...

that are divisible by p. The digamma function is the logarithmic derivative of the gamma function. Just as the gamma function provides a continuous interpolation...

than the negative integers x. The interpolating function is in fact closely related to the digamma function H x = ψ ( x + 1 ) + γ , {\displaystyle H_{x}=\psi...

x-\gamma } . Evaluations of the digamma function at rational values. The Laurent series expansion for the Riemann zeta function*, where it is the first of...

than zero, and E[ln X] = ψ(α) + ln θ = ψ(α) − ln λ is fixed (ψ is the digamma function). The parameterization with α and θ appears to be more common in econometrics...

Chebyshev function ψ ( x ) {\displaystyle \psi (x)} the polygamma function ψ m ( z ) {\displaystyle \psi ^{m}(z)} or its special cases the digamma function ψ...

multiplied by ln(z), plus another series in powers of z, involving the digamma function. See Olde Daalhuis (2010) for details. Around z = 1, if c − a − b is...

\end{aligned}}} where ψ ( α ) {\displaystyle \psi (\alpha )} is the digamma function. The Kullback-Leibler divergence of Inverse-Gamma(αp, βp) from Inverse-Gamma(αq...

Euler-Mascheroni constant, and ψ ( ⋅ ) {\displaystyle \psi (\cdot )} is the digamma function. In the case of equal rate parameters, the result is an Erlang distribution...

_{0})} where ψ {\displaystyle \psi } is the digamma function, ψ ′ {\displaystyle \psi '} is the trigamma function, and δ i j {\displaystyle \delta _{ij}}...

symbols in mathematics, in particular for ε/ϵ and π/ϖ. The archaic letter digamma (Ϝ/ϝ/ϛ) is sometimes used. The Bayer designation naming scheme for stars...

negative real axis, the first local maxima and minima (zeros of the digamma function) are: The only values of x > 0 for which Γ(x) = x are x = 1 and x ≈...

{\displaystyle \Gamma } is the gamma function and ψ = Γ ′ / Γ {\displaystyle \psi =\Gamma '/\Gamma } is the digamma function. As a special case, γ 0 ( 1 ) =...

example is the classical Poincaré-type asymptotic expansion of the digamma function ψ. ψ ( z ) ∼ ln ⁡ z − ∑ k = 1 ∞ B k + k z k {\displaystyle \psi (z)\sim...

(x)\psi (x),\end{aligned}}} with ψ ( x ) {\textstyle \psi (x)} being the digamma function, expressed by the parenthesized expression to the right of Γ ( x )...

(k)x^{k-1}=-\psi _{0}(1-x)-\gamma } where ψ 0 {\displaystyle \psi _{0}} is the digamma function. ∑ k = 2 ∞ ( ζ ( k ) − 1 ) = 1 ∑ k = 1 ∞ ( ζ ( 2 k ) − 1 ) = 3 4 ∑...

{\displaystyle \psi (k)={\frac {\Gamma '(k)}{\Gamma (k)}}\!} is the digamma function. Solving the first equation for p gives: p = N r N r + ∑ i = 1 N k...

Melchior Islands, Antarctica Chebyshev function Dedekind psi function Digamma function Polygamma functions Stream function, in two-dimensional flows Polar tangential...

\psi } is the digamma function Γ′/Γ. Roughly speaking, the explicit formula says the Fourier transform of the zeros of the zeta function is the set of...

needed] The digamma function, and by extension the polygamma function, is defined in terms of the logarithmic derivative of the gamma function. Generalizations...