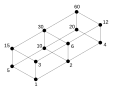
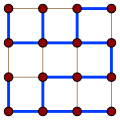
In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem states that, in any finite partially ordered set, the maximum size of...

orders the two theorems differ, and (as Mirsky observes) Dilworth's theorem is more difficult to prove. Mirsky's theorem and Dilworth's theorem are also related...

Philadelphia, Pennsylvania Robert P. Dilworth, mathematician Thomas Dilworth, English cleric Dilworth's theorem in mathematics Dilworth School in Auckland, New Zealand...

the proofs uses Dilworth's theorem on chain decompositions in partial orders, or its simpler dual (Mirsky's theorem). To prove the theorem, define a partial...

König's theorem Menger's theorem (1927) The max-flow min-cut theorem (Ford–Fulkerson algorithm) The Birkhoff–Von Neumann theorem (1946) Dilworth's theorem. In...

In mathematics, Kruskal's tree theorem states that the set of finite trees over a well-quasi-ordered set of labels is itself well-quasi-ordered under...

important minimax theorems in combinatorics, including Dilworth's theorem and Mirsky's theorem on partially ordered sets, Kőnig's theorem on matchings, and...

largest antichain in a partially ordered set is known as its width. By Dilworth's theorem, this also equals the minimum number of chains (totally ordered subsets)...

theorem can be used to prove Dilworth's theorem from the (much easier) proof of Mirsky's theorem, or vice versa. To prove the perfect graph theorem,...

such as Hall's marriage theorem and Dilworth's theorem. Since bipartite matching is a special case of maximum flow, the theorem also results from the max-flow...

of choice. Its applications include extending the four-color theorem and Dilworth's theorem from finite graphs and partially ordered sets to infinite ones...

isomorphism theorem (order theory) Dilworth's theorem (combinatorics, order theory) Four functions theorem (combinatorics) Hahn embedding theorem (ordered...

{\displaystyle n_{1},n_{2},\dots ,n_{p}.} Mathematics portal Dilworth's theorem Erdős–Ko–Rado theorem Anderson, Ian (1987), Combinatorics of Finite Sets, Oxford...

In mathematics, the Boolean prime ideal theorem states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement...

known for Dilworth's theorem (Dilworth 1950) relating chains and antichains in partial orders; he was also the first to study antimatroids (Dilworth 1940)...

{\displaystyle (Tu-Tv,u-v)\geq 0\quad \forall u,v\in X.} Kachurovskii's theorem shows that convex functions on Banach spaces have monotonic operators as...

is Mirsky's theorem, and the perfection of their complements is Dilworth's theorem; these facts, together with the perfect graph theorem can be used to...

graph Logic gate Boolean analysis Boolean prime ideal theorem Compactness theorem Consensus theorem De Morgan's laws Duality (order theory) Laws of classical...

& Tamassia (1995a), Theorem 9, p. 118; Baker, Fishburn & Roberts (1971), theorem 4.1, page 18. Garg & Tamassia (1995a), Theorem 15, p. 125; Bertolazzi...

further structure. Another early representation theorem is now known as Stone's representation theorem for distributive lattices (the name honors Marshall...

In set theory and order theory, the Cantor–Bernstein theorem states that the cardinality of the second type class, the class of countable order types...

set I such that I contains exactly one vertex from each path in P. Dilworth's theorem follows as a corollary of this result. Given a directed graph G, the...

without the axiom of choice). This issue is discussed in various prime ideal theorems, which are necessary for many applications that require prime ideals. An...

Gallai also proved, with Milgram, Dilworth's theorem in 1947, but as they hesitated to publish the result, Dilworth independently discovered and published...

Results Boolean prime ideal theorem Cantor–Bernstein theorem Cantor's isomorphism theorem Dilworth's theorem Dushnik–Miller theorem Hausdorff maximal principle...

number, called the order type of the well-ordered set. The well-ordering theorem, which is equivalent to the axiom of choice, states that every set can...

countable intersections of open sets are open Speer 2007, Theorem 7. Arenas 1999, Theorem 2.2. Erné, M. "The ABC of order and topology" (PDF)., page...

partial orders, called distributive lattices; see Birkhoff's representation theorem. Sequence A001035 in OEIS gives the number of partial orders on a set of...

Results Boolean prime ideal theorem Cantor–Bernstein theorem Cantor's isomorphism theorem Dilworth's theorem Dushnik–Miller theorem Hausdorff maximal principle...

the proofs of several theorems of crucial importance, for instance the Hahn–Banach theorem in functional analysis, the theorem that every vector space...