In the mathematics of convergent and divergent series, Euler summation is a summation method. That is, it is a method for assigning a value to a series...

Bernoulli functions. Cesàro summation Euler summation Gauss–Kronrod quadrature formula Darboux's formula Euler–Boole summation Apostol, T. M. (1 May 1999)...

} Ramanujan summation is a method of assigning a value to divergent series used by Ramanujan and based on the Euler–Maclaurin summation formula. The...

Integration using Euler's formula Euler summation Euler–Boole summation Euler angles defining a rotation in space Euler brick Euler's line – relation between...

Divergent series Euler summation Euler–Boole summation Fejér's theorem Hölder summation Lambert summation Perron's formula Ramanujan summation Riesz mean Silverman–Toeplitz...

special case of Mittag-Leffler summation with α = 1. (wB) can be seen as the limiting case of generalized Euler summation method (E,q) in the sense that...

Euler–Boole summation is a method for summing alternating series. The concept is named after Leonhard Euler and George Boole. Boole published this summation...

Euler–Maclaurin formula. For summations in which the summand is given (or can be interpolated) by an integrable function of the index, the summation can...

summation functions as a property of partial sums. If we take the Euler–Maclaurin summation formula together with the correction rule using Bernoulli numbers...

Chapter 14: Euler's derivation of the Euler–Maclaurin summation formula. Mills, Stella (1985). "The independent derivations by Leonhard Euler and Colin...

In the calculus of variations and classical mechanics, the Euler–Lagrange equations are a system of second-order ordinary differential equations whose...

interpretations of Euler's attempts. Many of these summability methods easily assign to 1 − 2 + 3 − 4 + ... a "value" of ⁠1/4⁠. Cesàro summation is one of the...

conjectured by Konrad Knopp in 1926 and proven by Helmut Hasse in 1930 (cf. Euler summation): ζ ( s ) = 1 1 − 2 1 − s ∑ n = 0 ∞ 1 2 n + 1 ∑ k = 0 n ( n k ) ( −...

}t^{z-1}e^{-t}\,dt} converges absolutely, and is known as the Euler integral of the second kind. (Euler's integral of the first kind is the beta function.) Using...

approach; today one says that 1 − 2 + 4 − 8 + ... is Euler-summable and that its Euler sum is ⁠1/3⁠. The Euler transform begins with the sequence of positive...

(also known as the Einstein summation convention or Einstein summation notation) is a notational convention that implies summation over a set of indexed terms...

with its reliance on complex analysis, and Ramanujan summation, with its shortcut to the Euler–Maclaurin formula. Instead, the method operates directly...

In mathematics and computational science, the Euler method (also called the forward Euler method) is a first-order numerical procedure for solving ordinary...

Bernoulli umbra Bell number Euler number Genocchi number Kummer's congruences Poly-Bernoulli number Hurwitz zeta function Euler summation Stirling polynomial...

become much smaller, much more rapidly, thus allowing rapid numerical summation. The Euler transform can be generalized (Borisov B. and Shkodrov V., 2007):...

577 … {\displaystyle \gamma _{0}=\gamma =0.577\dots } Euler–Lehmer constants are given by summation of inverses of numbers in a common modulo class: γ (...

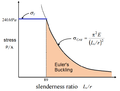
Euler's critical load or Euler's buckling load is the compressive load at which a slender column will suddenly bend or buckle. It is given by the formula:...

series acceleration techniques. One of the oldest techniques is that of Euler summation, and there are many modern techniques that can offer even more rapid...

Arithmetica Infinitorum. Hypergeometric series were studied by Leonhard Euler, but the first full systematic treatment was given by Carl Friedrich Gauss (1813)...

Abel summation Cesàro summation Lindelöf summation Euler summation Borel summation Mittag-Leffler summation Lambert summation Euler–Boole summation and...

Cesàro summation Euler summation Lambert summation Borel summation Summation by parts – transforms the summation of products of into other summations Cesàro...

fluid mechanics and astrophysics, the relativistic Euler equations are a generalization of the Euler equations that account for the effects of general...

a finite decimal fraction. The formula is a special case of the Euler–Boole summation formula for alternating series, providing yet another example of...

finance. Among the Ancient Greeks, the idea that a potentially infinite summation could produce a finite result was considered paradoxical, most famously...

assigned a value of approximately 0.596347 by Borel summation. This series was first considered by Euler, who applied summability methods to assign a finite...